Q 1 – The prime factorisation of 13915 is
a) 5 × 113 × 132
b) 5 × 113 × 232
c) 5 × 112 × 23
d) 5 × 112 × 132
Ans – c) 5 × 112 × 23
Q 2 – A Mathematics Exhibition is being conducted in your School and one of your friends is making a model of a factor tree. He has some difficulty and asks for your help in completing a quiz for the audience.
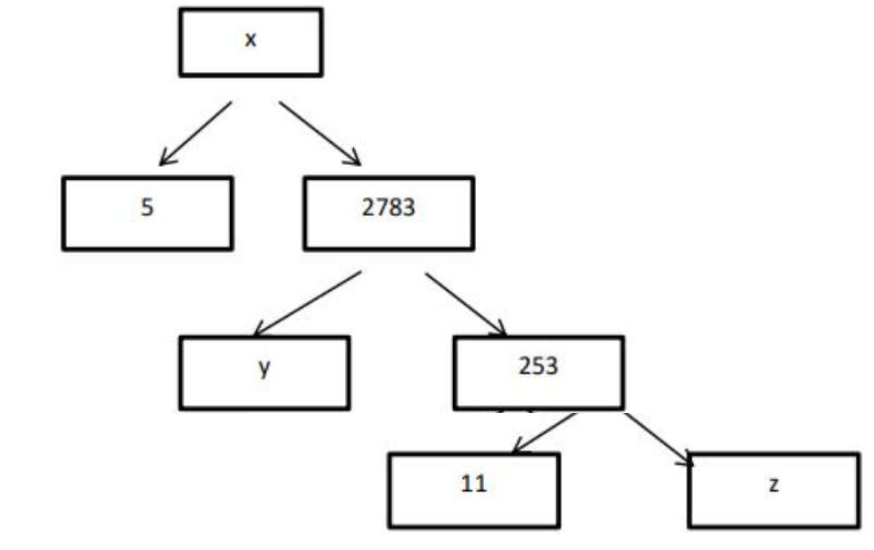
Observe the following factor tree and answer the following:
1. What will be the value of x ?
a) 15005
b) 13915
c) 56920
d) 17429
Ans – b) 13915
2. What will be the value of Z ?
a) 22
b) 23
c) 17
d) 19
Ans – b) 23
Q 3 – The product of HCF and LCM of 60, 84, and 108 is
a) 55360
b) 35360
c) 45500
d) 45360
Ans – d) 45360
Q 4 – A seminar is being conducted by an Educational Organisation, where the participants will be educators of different subjects. The number of participants in Hindi, English and Mathematics are 60, 84 and 108 respectively.
In each room the same number of participants are to be seated and all of them being in the same subject, hence maximum number participants that can accommodated in each room are
a) 14
b) 12
c) 16
d) 18
Ans – b) 12
2. What is the minimum number of rooms required during the event?
a) 11
b) 31
c) 41
d) 21
Ans – d) 21
Q 5 – For any two positive integers a and b, there exist (unique) whole numbers q and r such that
(a) q = ar + b , 0 ⩽ r < b.
(b) a = bq + r , 0 ⩽ r < b.
(c) b = aq + r , 0 ⩽ r < b.
(d) none of these
Ans – b) a = bq + r , 0 ⩽ r < b.
Q 6 – The least number that is divisible by all the numbers from 1 to 8 (both inclusive) is
(a) 840
(b) 2520
(c) 8
(d) 420
Ans – a) 840
Q 7 – For positive integers a and 3, there exist unique integers q and r such that a = 3q + r, where r must satisfy:
(a) 0 < r < 3
(b) 1 < r < 3
(c) 0 < r < 3
(d) 0 < r < 3
Ans – (a) 0 < r < 3

Ans –
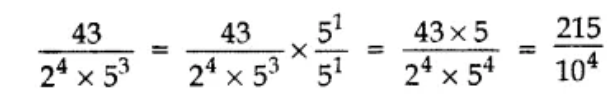
After 4 decimal places.
Q 9 – If the HCF of 408 and 1032 is expressible in the form 1032 * 2 + 408 p, then find the value of p.
Ans –
HCF of 408 and 1032 is 24.
1032 × 2 + 408 × (p) = 24
408p = 24 – 2064
p = – 5
Q 10 – The decimal expansion of π is:
- Terminating
- Non-terminating and Non-recurring
- Non-terminating and recurring
- Doesn’t exist
Ans- c) Non-terminating and recurring
Q 11 – Find the largest number that will divide 398, 436 and 542 leaving remainders 7, 11, and 15 respectively.
Ans –
Algorithm
398 – 7 = 391, 436 – 11 = 425, 542 – 15 = 527
HCF of 391, 425, 527 = 17
Q 12 – Which of the following rational numbers have a terminating decimal expansion?
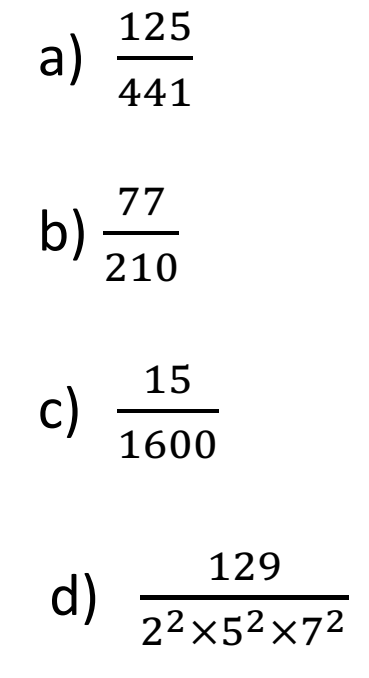
Ans- (c)
Q 13 – HCF and LCM of two numbers are 9 and 459 respectively. If one of the numbers is 27, find the other number.
Ans –
We know,
1st number × 2nd number = HCF × LCM
⇒ 27 × 2nd number = 9 × 459
⇒ 2nd number = 153
Q 14 – Find LCM of numbers whose prime factorisation is expressible
as 3 × 52 and 32 × 72.
Ans –
LCM is the multiplication of the highest powers of prime factors of the numbers.
(3 x 52 , 32 x 72) = 32 x 52 x 72 = 9 x 25 x 49 = 11025
Q 15 – Find the HCF (865, 255) using Euclid’s division lemma.
Ans –
As 865 > 255 take 865 as ‘a’ and 255 as ‘b’ .
865 = 255 × 3 + 100
255 = 100 × 2 + 55
100 = 55 × 1 + 45
55 = 45 × 1 + 10
45 = 10 × 4 + 5
10 = 5 × 2 + 0
The remainder is 0.
HCF = 5

Ans –
Let us assume, to the contrary, that 2 + 3√5 is rational.
So that we can find integers a and b (b ≠ 0).
Such that 2 + 3√5 = , where a and b are coprime.
Rearranging the above equation, we get
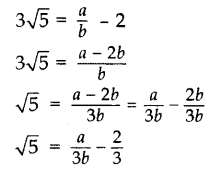
Since a and b are integers, we get is rational and so √5 is rational.
But this contradicts the fact that √5 is irrational.
So, we conclude that 2 + 3√5 is irrational.
Q 17 – Check whether 4n can end with the digit 0 for any natural number n.
Ans –
4n = (22)n = 22n
The only prime in the factorization of 4n is 2.
There is no other prime in the factorization of 4n = 2n
(By uniqueness of the Fundamental Theorem of Arithmetic).
5 does not occur in the prime factorization of 4n for any n.
Therefore, 4n does not end with the digit zero for any natural number n.

Ans –
Step-by-step explanation:
To prove :√5 is irrational number.
Proof :
Let us assume that √5 is rational
Then √5 = a/b
(a and b are co primes, with only 1 common factor and b≠0)
⇒ √5 = a/b
(cross multiply)
⇒ a = √5b , Taking squares on both sides.
⇒ a² = 5b² …………………. eq.(1)
⇒ 5 is a factor of a² from eq.(1)
(by theorem if p divides q then p can also divide q²)
⇒ 5 is a factor of a (Theorem) eq.(2)
⇒ a = 5c (where c is an integer )
(squaring on both sides)
⇒ a² = 25c² …………………. eq.(3)
From equations eq.(1) and eq.(3)
⇒ 5b² = 25c²
⇒ b² = 5c²
⇒ 5 is a factor of b² from
(by theorem if p divides q then p can also divide q²)
⇒ 5 is a factor of b (Theorem) eq.(4)
We know that a and b are co-primes having only 1 common factor but from eq.(2) and eq.(4) we can say that it is wrong and 5 is also common factor of a & b .
This contradiction arises because we assumed that √5 is a rational number
∴ Our assumption is wrong
∴ √5 is irrational number
Part-b) Let us assume that 3 + √5 is a rational number.
Now,
3 + √5 = p/q
[Here p and q are co-prime numbers]
√5 = [p/q] – 3
√5 = [p/q] – 3
Here, [p/q] – 3 is a rational number.
But we know that √5 is a irrational number but [p/q] – 3 is a rational number. We know that LHS = RHS.
So, [p/q] – 3 is also a irrational number.
So, our assumption is wrong.
3 + √5 is a irrational number.
Hence, proved.
Q 19 – Two tankers contain 850 liters and 680 liters of petrol. Find the maximum capacity of a container that can measure the petrol of each tanker the exact number of times.
Ans –
To find the maximum capacity of a container which can measure the petrol of each tanker in the exact number of times, we find the HCF of 850 and 680.
850 = 2 × 52 × 17
680 = 23 × 5 × 17
HCF = 2 × 5 × 17 = 170
Maximum capacity of the container = 170 liters.

Q 20 – By using Euclid’s algorithm, find the largest number which divides 650 and 1170.
Ans –
Given numbers are 650 and 1170.
1170 > 650
1170 = 650 × 1 + 520
650 = 520 × 1 + 130
520 = 130 × 4 + 0
HCF = 130
The required largest number is 130.
Q 21 – The length, breadth, and height of a room are 8 m 50 cm, 6 m 25 cm, and 4 m 75 cm respectively. Find the length of the longest rod that can measure the dimensions of the room exactly.
Ans-
Length of room = 8m 25cm = 825 cm
Breadth of room = 6m 75m = 675 cm
Height of room = 4m 50m = 450 cm
∴ The required longest rod
= HCF of 825, 675 and 450
First consider 675 and 450
By applying Euclid’s division lemma
675 = 450 × 1 + 225
450 = 225 × 2 + 0
∴ HCF of 675 and 450 = 825
Now consider 625 and 825
By applying Euclid’s division lemma
825 = 225 × 3 + 150
225 = 150 × 1 + 75
150 = 75 × 2 + 0
HCF of 825, 675 and 450 = 75
Q 22 – If two positive integers x and y are expressible in terms of primes as x = p2 q3 and y = p3q, what can you say about their LCM and HCF. Is LCM a multiple of HCF? Explain.
Ans –
x = p2q3 and y = p3q
LCM = p3q3
HCF = p2q …..(i)
Now, LCM = p3q3
⇒ LCM = pq2 (p2q)
⇒ LCM = pq2 (HCF)
Yes, LCM is a multiple of HCF.
Explanation:
Let a = 12 = 22 × 3
b = 18 = 2 × 32
HCF = 2 × 3 = 6 …(ii)
LCM = 22 × 32 = 36
LCM = 6 × 6
LCM = 6 (HCF) …[From (ii)]
Here LCM is 6 times HCF.
Q 23 – Find the HCF and LCM of 306 and 657 and verify that LCM × HCF = Product of the two numbers.
Ans –
306 = 2 × 32 × 17
657 = 32 × 73
HCF = 32 = 9
LCM = 2 × 32 × 17 × 73 = 22338
L.H.S. = LCM × HCF = 22338 × 9 = 201042
R.H.S. = Product of two numbers = 306 × 657 = 201042
L.H.S. = R.H.S
Q 24 – Find whether decimal expansion of 13/64 is a terminating or non-terminating decimal.If it terminates, find the number of decimal places its decimal expansion has.
Ans –

Q 25 – Floor of a room is to be fitted with square marble tiles of the largest possible size. The size of the room is 10 m by 7 m. What should be the size of tiles required that has to be cut and how many such tiles are required?
Ans –
Least number of square tiles are required if the side of the square tile is the H.C.F. of the length and breadth.
length of the room = 10 m
Breadth of the room = 7 m
H.C.F. of 10 and 7
10 = (7 x 1) + 3
7 = (3 x 2) + 1
3 = (1 x 3) + 0
So, H.C.F. of 10 and 7 is 1
Therefore, the length of the square tile is 1 m
Area of 1 square tile = 1 x 1 = 1 sq m
Area of the room = 10 x 7 = 70 sq m
Number of square tile required each measuring 1m × 1m = 70/1
= 70 tiles
Hence, the size of each square tile is 1m x 1m and 70 square tiles will be required.
Q 26 – The LCM of 2 numbers is 14 times their HCF. The sum of LCM and HCF is 600. If one number is 280, then find the other number.
Ans –
Given, One no. is 280
Let, HCF be x
so LCM = 14x
Sum of HCF and LCM = 600
x + 14x = 600
15x = 600
So, HCF = 40
LCM = 14 x 40 = 560
To Find Other no. –
first no. = 280
second no. = y
We Know that
HCF x LCM = product of two numbers
40 × 560 = 280 × y
22400 = 280y
y = 22400 / 280