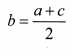NCERT SOLUTIONS FOR CLASS 10 MATHS ARITHMETIC PROGRESSIONS CHAPTER 5 EX 5.1

NCERT SOLUTIONS FOR CLASS 10 MATHS ARITHMETIC PROGRESSIONS CHAPTER 5 EX 5.1

Question 1.
In which of the following situations, does the list of numbers involved make an arithmetic progression and why?
(i) The taxi fare after each km when the fare is ₹ 15 for the first km and ₹ 8 for each additional km.
(ii) The amount of air present in a cylinder when a vacuum pump removes 14 of the air remaining in the cylinder at a time.
(iii) The cost of digging a well after every meter of digging, when it costs ₹ 150 for the first meter and rises by ₹ 50 for each subsequent meter.
(iv) The amount of money in the account every year, when ₹ 10000 is deposited at compound interest at 8% per annum.
Solution:

Ex 5.1 Class 10 Maths Question 2.
Write first four terms of the AP, when the first term a and the common difference d are given as follows:
(i) a = 10, d = 10
(ii) a = -2, d = 0
(iii) a = 4, d = -3
(iv) a = -1, d = 12
(v) a = -1.25, d = -0.25
Solution:

Ex 5.1 Class 10 Maths Question 3.
For the following APs, write the first term and the common difference:
(i) 3, 1, -1, -3, ……
(ii) -5, -1, 3, 7, ……
(iii) 13 , 53 , 93, 133 , ……..
(iv) 0.6, 1.7, 2.8, 3.9, …….
Solution: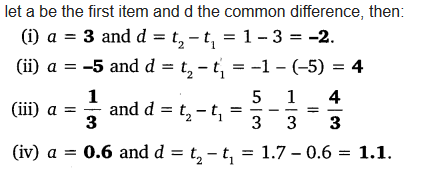

Ex 5.1 Class 10 Maths Question 4.
Which of the following are APs ? If they form an AP, find the common difference d and write three more terms.
(i) 2, 4, 8, 16, …….
(ii) 2, 52 , 3, 72 , …….
(iii) -1.2, -3.2, -5.2, -7.2, ……
(iv) -10, -6, -2,2, …..
(v) 3, 3 + 2–√, 3 + 22–√, 3 + 32–√, …..
(vi) 0.2, 0.22, 0.222, 0.2222, ……
(vii) 0, -4, -8, -12, …..
(viii) −12 , −12 , −12 , −12 , …….
(ix) 1, 3, 9, 27, …….
(x) a, 2a, 3a, 4a, …….
(xi) a, a2, a3, a4, …….
(xii) 2–√, 8–√, 18−−√, 32−−√, …..
(xiii) 3–√, 6–√, 9–√, 12−−√, …..
(xiv) 12, 32, 52, 72, ……
(xv) 12, 52, 72, 73, ……
Solution:

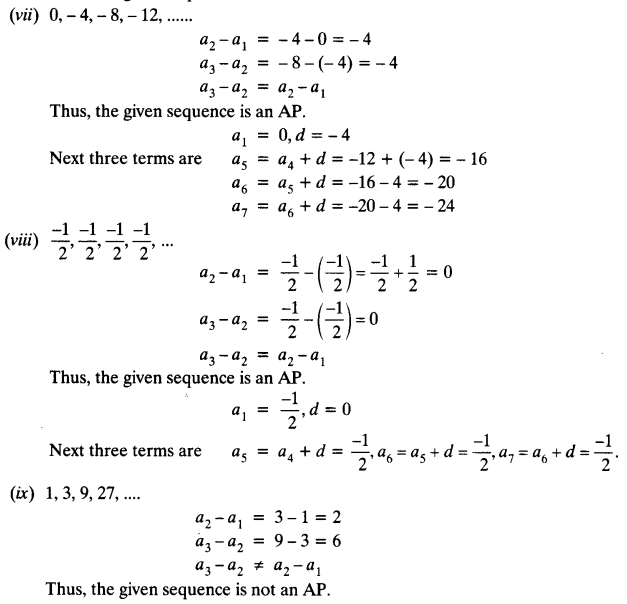
Class 10 Maths Arithmetic Progressions Mind Maps

Arithmetic Progression (AP)

Consider
(i) 1, 2, 3, 4, ……
(ii) 3, 3, 3, 3, …..
(i) and (ii) are the sequence of numbers, each number in these sequences is called a term.

An arithmetic progression (AP) is a sequence of numbers in which each term is obtained by adding a fixed number ‘d’ to the preceeding term, except the first term.
The fixed number is called the common difference. It can be positive, negative or zero.
Any Arithmetic progression can be represented as :
a, a + d, a + 2d, a + 3d,…..
where ‘a’ is the first term and ‘d’ is the common difference. Arithmetic progressions which does not have a last term are called Infinite Arithmetic Progression. e.g.:
6, 9, 12, 15,…….

Formula for common Difference (d)

A sequence of numbers a₁, a₂, a₃…. is an AP if the difference a₂ – a₁, a₃ – a₂, a₄ – a₃…. gives the same value, i.e. if a_k+1 – a_k is the same for different values of k. The difference (a_k+1 – a_k) is called common difference (d). Here a_k+1 and a_k are the (k + 1)th and kth terms respectively.
∴ d = a₂ – a₁ = a₃ – a₂ = a₄ – a₃

n^th Term (or General Term) of an Arithmetic Progressions

In an AP, with first term ‘a’ and common difference d, the n^th term(or the general term) is given by,
a_n = a + (n – 1)d
Note that an AP can be finite or infinite according to as the number of terms are finite or infinite.
If there are m terms in an AP then a_m is the last term and is sometimes denoted by ‘l’.

Sum of the FIRST ‘n’ Terms of an A.P.

(i) The sum of the first n terms of an A.P. is given by

where a is the first term and d is the common difference
(ii) If l is the last term of the finite A.P. say the n^th term, then the sum of all terms of the A.P. is given by,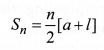

Note that sum of first n positive integers is given by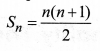

Arithmetic Mean Between Two Numbers

If a, b, c are in AP. Then b is called the arithmetic mean of a and c and is given by