NCERT SOLUTIONS FOR CLASS 10 MATHS INTRODUCTION TO TRIGONOMETRY CHAPTER 8 EX 8.1

NCERT SOLUTIONS FOR CLASS 10 MATHS INTRODUCTION TO TRIGONOMETRY CHAPTER 8 EX 8.1

Question 1.
In ∆ABC right angled at B, AB = 24 cm, BC = 7 cm. Determine:
(i) sin A, cos A
(ii) sin C, cos C
Solution: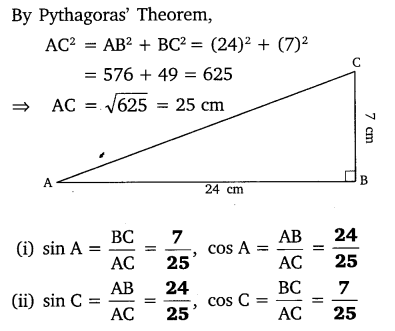

Ex 8.1 Class 10 Maths Question 2.
In given figure, find tan P – cot R.
Solution:

Ex 8.1 Class 10 Maths Question 3.
If sin A = 34 , calculate cos A and tan A.
Solution: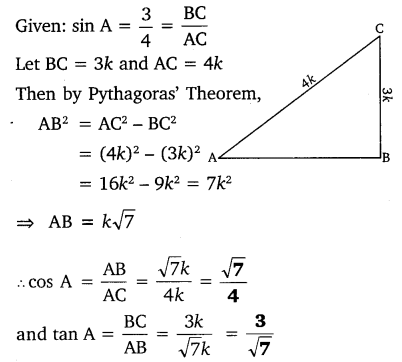

Ex 8.1 Class 10 Maths Question 4.
Given 15 cot A = 8, find sin A and sec A.
Solution:

Ex 8.1 Class 10 Maths Question 5.
Given sec θ = 1312 , calculate all other trigonometric ratios.
Solution:

Ex 8.1 Class 10 Maths Question 6.
If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
Solution:

Ex 8.1 Class 10 Maths Question 7.
If cot θ = 78, evaluate:
(i) (1+sinθ)(1−sinθ)(1+cosθ)(1−cosθ)
(ii) cot²θ
Solution:

Ex 8.1 Class 10 Maths Question 8.
If 3 cot A = 4, check whether 1−tan2A1+tan2A = cos² A – sin² A or not.

Ex 8.1 Class 10 Maths Question 9.
In triangle ABC, right angled at B, if tan A = 1√3, find the value of:
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C
Solution:

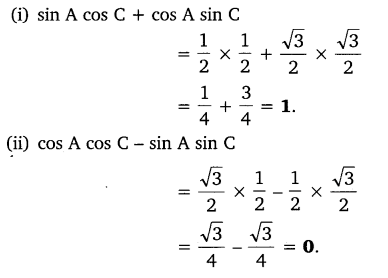
Ex 8.1 Class 10 Maths Question 10.
In ΔPQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
Solution:

Ex 8.1 Class 10 Maths Question 11.
State whether the following statements are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
(ii) sec A = 125 for some value of angle A.
(iii) cos A is the abbreviation used for the cosecant of angle A.
(iv) cot A is the product of cot and A.
(v) sin θ = 43 for some angle.
Solution:

Class 10 Maths Introduction To Trigonometry

Trigonometry

Trigonometry is the study of relationships between the sides and angles of a right-angled triangle.

Trigonometric Ratios

Trigonometric ratios of an acute angle in a right triangle express the relationship between the angle and the length of its sides.
Let ∆ABC be a triangle right angled at B. Then the trigonometric ratios of the angle A in right ∆ABC are defined as follows: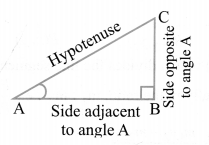

Note:
The values of the trigonometric ratios of an angle do not vary with the lengths of the sides of the triangle, if the angle remains same.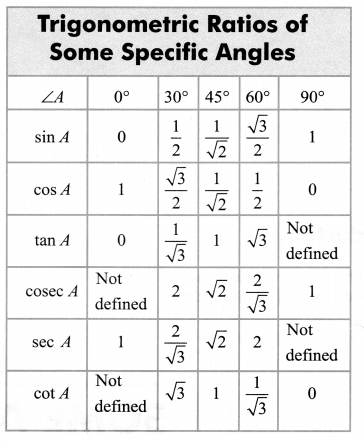

Trigonometric Ratios for Complementary Angles

sin (90° – A) = cos A
cos (90° – A) = sin A
tan (90° – A) = cot A
cot (90° – A) = tan A
sec (90° – A) = cosec A
cosec (90° – A) = sec A
Note:
Here (90° – A) is the complementary angle of A.

Trigonometric Identities

An equation involving trigonometric ratios of an angle is called a trigonometric identity, if it is true for all values of the angle(s) involved.
(i) sin²θ + cos²θ = 1 [for 0° ≤ θ ≤ 90°]
(ii) sec²θ – tan²θ = 1 [for 0° ≤ θ ≤ 90°]
(iii) cosec²θ – cot²θ = 1 [for 0° < θ ≤ 90°]