Q 1 – A line that intersects two or more lines at distinct points is called
(a) parallel
(b) transversal
(c) intersecting
(d) None of these
Ans– (b) transversal
Q 2 – When the sum of the measures of two angles is 90°, the angles are called
(а) supplementary angles
(b) complementary angles
(c) adjacent angles
(d) vertically opposite angles
Ans– (b) complementary angles
Q 3 – Which of the following statements is true?
(a) Two acute angles can be supplementary.
(b) Two right angles can be supplementary.
(c) Two obtuse angles can be supplementary.
(d) One obtuse angle and one acute angle cannot be supplementary.
Ans– (b) Two right angles can be supplementary.
Q 4 – The measure of the angle which is equal to its supplement is
(a) 30°
(b) 45°
(c) 90°
(d) 60°
Ans– (c) 90°
Hint:
x° + x° = 180° ⇒ x° = 90°.
Q 5 – What happens to the measurement of an angle after the extension of its arms?
(a) Doubles
(b) Triples
(c) Remains the same
(d) Cannot be said.
Ans– (c) Remains the same
Q 6 – Which of the following pairs of angles is not a pair of supplementary angles?
(a) 90°, 90°
(b) 32°, 58°
(c) 0°, 180°
(d) 76°, 104°
Ans– (b) 32°, 58°
Hint:
32° + 58° = 90° ≠ 180°.
Q 7 – Find the angle, which is equal to its supplement.
(a) 60°
(b) 90°
(c) 120°
(d) 30°
Ans– (b) 90°
Q 8 – Which of the following pairs of angles form a linear pair?
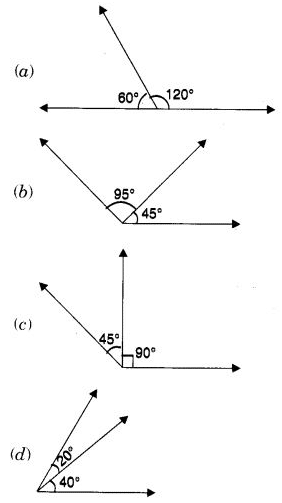
Ans– (a)
Hint:
120° + 60° = 180°.
Q 9 – The measure of the complement of the angle 30° is
(а) 30°
(b) 90°
(c) 60°
(d) 160°
Ans– (c) 60°
Q 10 – What is the supplement of 105°
(a) 65°
(b) 75°
(c) 85°
(d) 95°
Ans– (b) 75°
Q 11 – Which of the following statements is false?
(a) Two vertically opposite angles can be acute
(b) Two vertically opposite angles can be obtuse
(c) Two vertically opposite angles can be right angles
(d) Two vertically opposite angles may be unequal
Ans– (d) Two vertically opposite angles may be unequal
Q 12 – What do we call an angle whose measurement is exactly equal to 0°?
(a) An obtuse angle
(b) A straight angle
(c) A zero angle
(d) A right angle
Ans– (c) A zero angle
Q 13 – Which of the following statements is true?
(a) Two acute angles can be complementary to each other
(b) Two obtuse angles can be complementary to each other
(c) Two right angles can be complementary to each other
(d) One obtuse angle and one acute angle can be complementary to each other.
Ans– (a) Two acute angles can be complementary to each other.
Q 14 – Identity which of the following pairs of angles are complementary.
(a) 65°, 115°
(b) 130°, 50°
(c) 63°, 27°
(d) 112°, 68°
Ans– (c) 63°, 27°
Q 15 – If two lines intersect at a point, then the vertically opposite angles are always ________
(a) supplementary
(b) equal
(c) unequal
(d) none of these
Ans– (b) equal
Q 16 – What are the lines which lie on the same plane and do not intersect at any point called?
(a) Perpendicular lines
(b) Intersecting lines
(c) Parallel lines
(d) Collinear lines
Ans– (c) Parallel lines
Q 17 – If two angles are supplementary then the sum of their measures is __________.
(a) 45°
(b) 180°
(c) 90°
(d) 360°
Ans– (b) 180°
Q 18 – Which of the following statements is false?
(a) When a transversal cuts two parallel lines, each pair of corresponding angles are equal.
(b) When a transversal cuts two parallel lines, each pair of alternate interior angles are equal.
(c) When a transversal cuts two parallel lines, each pair of interior angles on the same side of the transversal are supplementary.
(d) A transversal cuts two parallel lines in three points.
Ans– (d) A transversal cuts two parallel lines in three points.
Q 19 – In the following figure, ∠ AOB and ∠ BOC are
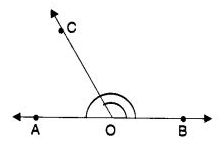
(a) complementary angles
(b) supplementary angles
(c) adjacent angles
(d) none of these
Ans– (d) None of these
Q 20 – The measure of the complement of the angle 46° is
(a) 90°
(b) 44°
(c) 16°
(d) 136°
Ans– (b) 44°
Hint:
Complementary angle = 90° − given angle
⇒ Complement of 46° = 90° − 46° = 44°
Q 21 – In the following figure, reflex ∠ AOB is equal to
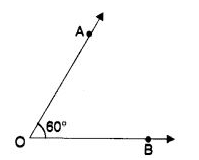
(a) 60°
(b) 120°
(c) 300°
(d) 360°
Ans– (c) 300°
Hint:
∠AOB = 360° – 60° = 300°
Q 22 – Which of the following statements is false?
(a) When a transversal cuts two lines, such that pairs of corresponding angles are equal, then the lines have to be parallel.
(b) When a transversal cuts two lines such that pairs of alternate interior angles are equal, then the lines have to be parallel.
(c) When a transversal cuts two lines such that pairs of interior angles on the same side of the transversal are supplementary, then the lines have to be parallel.
(d) When a transversal cuts two lines such that pairs of interior angles on the same side of the transversal are complementary, then the lines have to be parallel.
Ans– (d) When a transversal cuts two lines such that pairs of interior angles on the same side of the transversal are complementary, then the lines have to be parallel.
Q 23 – What is the measure of the complement of 41°?
(a) 135°
(b) 15°
(c) 49°
(d) None of these
Ans– (c) 49°
Q 24 – In the following figure, two straight lines AB and CD are intersecting each other at point 0 and the angles thus formed at 0 are marked, then the value of ∠x – ∠y is
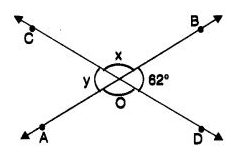
(a) 56°
(b) 118°
(c) 62°
(d) 180°
Ans– (a) 56°
Hint:
∠x – ∠y = (180° – 62°) – 62° = 118° – 62° = 56°.
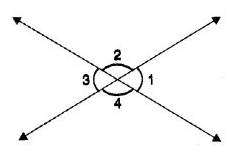
Q 25 – In the following figure, if ∠1 + ∠3 = 120°, then ∠2 + ∠4 is equal to
(a) 60°
(b) 120°
(c) 240°
(d) 80°
Ans– (c) 240°
Hint:
∠2 + ∠4 = 360° – (∠1 + ∠3) = 360° – 120° = 240°
Q 26 – What is the measure of the complement of the angle 80°?
(a) 10°
(b) 100°
(c) 36°
(d) 20°
Ans– (a) 10°
Hint:
90° – 80° = 10°.
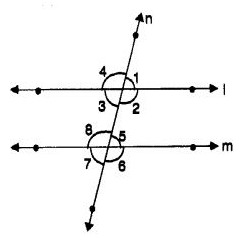
Q 27 – In the following figure, tell which pair of angles are not corresponding angles?
(a) ∠1, ∠5
(b) ∠2, ∠6
(c) ∠3, ∠7
(d) ∠3, ∠5
Ans– (d) ∠3, ∠5
Hint:
∠3, ∠5 are alternate interior angles.
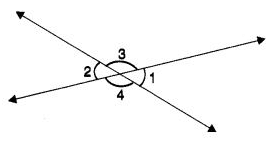
Q 28 – In the following figure, if ∠1 + ∠2 = 100°, then the measure of ∠4 is equal to
(a) 50°
(b) 100°
(c) 80°
(d) 130°
Ans– (d) 130°
Hint:
∠1 = ∠2; ∠1 + ∠2 = 100°
∴ ∠1 = 50°
∴ ∠4 = 180° – 50° = 130°.
Q 29 – Which pair of the following angles are complementary?
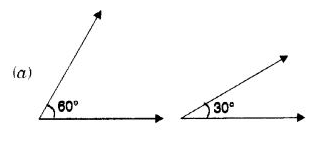
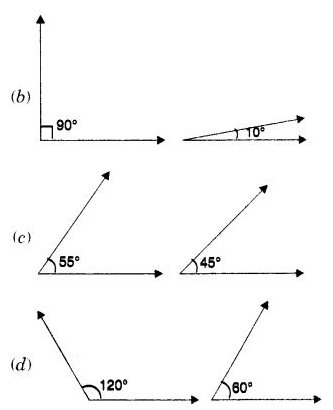
Ans– (a)
Hint:
60°+ 30° = 90°.
Q 30 – In the following figure, l || m. Find the measure of ∠ x.
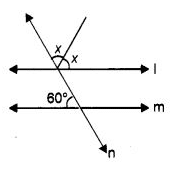
(a) 60°
(b) 45°
(c) 30°
(d) none of these
Ans– (a) 60°
Hint:
x + x + 60° = 180° ⇒ x = 60°.
Q 31 – How many rays can be drawn from a given point?
(a) 2
(b) 5
(c) 8
(d) Infinitely many
Ans– (d) Infinitely many
Q 32 – In the following figure, a transversal cuts two parallel lines l and m at points G and H respectively and the angles thus formed are marked. If ∠1 is an acute angle, then, which of the following statements is false?
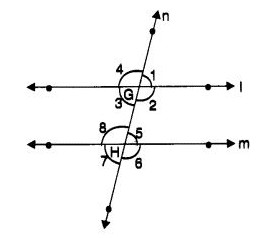
(а) ∠1 + ∠2 = 180°
(b) ∠2 + ∠5 = 180°
(c) ∠3 + ∠8 = 180°
(d) ∠2 + ∠6 = 180°
Ans– (d) ∠2 + ∠6 = 180°
Hint:
∠2 = ∠6, corresponding angles.
Q 33 – The measure of the angle which is equal to its complement is
(a) 30°
(b) 60°
(c) 46°
(d) 90°
Ans– (c) 46°
Hint:
x° + x° = 90° ⇒ x° = 45°.
Q 34 – Find the measure of the angle which is half of its supplementary angle?
(a) 60°
(b) 120°
(c) 90°
(d) 45°
Ans– (a) 60°
Hint:
x° = ½ (180° – x°) ⇒ x° = 60°.
Q 35 – In the following figure, AB || DG and BC || EF. Also, ∠ABC = 60°. Then, the measure of ∠DEF is
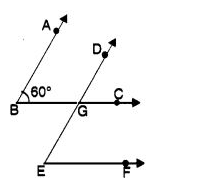
(a) 30°
(b) 60°
(c) 45°
(d) 120°
Ans– (b) 60°
Hint:
∠DEF = ∠DGC = ∠ABC = 60°.
Q 36 – Identity which of the following pairs of angles are supplementary.
(a) 45°, 45°
(b) 63°, 27°
(c) 112°, 68°
(d) 80°, 10°
Ans– (c) 112°, 68°
Q 37 – Find the value of x in the following figure, if l || m.
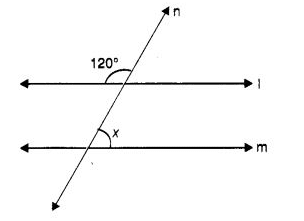
(a) 30°
(b) 45°
(c) 60°
(d) none of these
Ans– (c) 60°
Hint:
x + 120° = 180° ⇒ x = 60°.
Q 38 – Which of the following pairs of angles is not a pair of complementary angles?
(a) 60°, 30°
(b) 66°, 34°
(c) 0°, 90°
(d) 160°, 30°
Ans– (d) 160°, 30°
Hint:
150° + 30° = 180° ≠ 90°.
Q 39 – What is the measure of the complement of the angle 90°?
(а) 90°
(b) 0°
(c) 180°
(d) 46°
Ans– (b) 0°
Hint:
90° – 90° = 0°.
Q 40 – Find the angles which 1/ 5 are of its complement.
Ans– Let the required angle be x°
its complement = (90 – x)°
As per condition, we get
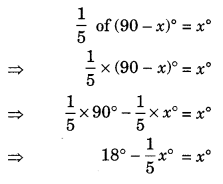
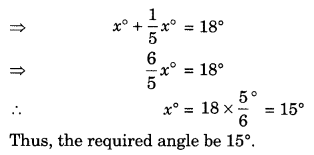
Q 41 – Find the angles which is 2 / 3 of its supplement.
Ans– Let the required angle be x°.
its supplement = (180 – x)°
As per the condition, we get
2 / 3 of (180 – x)° = x°
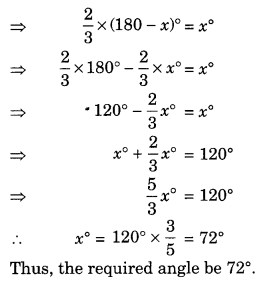
Q 42 – Find the value of x in the given figure.
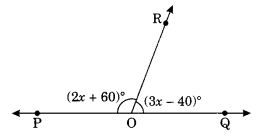
Ans–
∠POR + ∠QOR = 180° (Angles of linear pair)
⇒ (2x + 60°) + (3x – 40)° = 180°
⇒ 2x + 60 + 3x – 40 = 180°
⇒ 5x + 20 = 180°
⇒ 5x = 180 – 20 = 160
⇒ x = 32
Thus, the value of x = 32.
Q 43 – In the given figure, find the value of y.
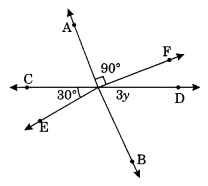
Ans–
Let the angle opposite to 90° be z.
z = 90° (Vertically opposite angle)
3y + z + 30° = 180° (Sum of adjacent angles on a straight line)
⇒ 3y + 90° + 30° = 180°
⇒ 3y + 120° = 180°
⇒ 3y = 180° – 120° = 60°
⇒ y = 20°
Thus the value of y = 20°.
Q 44 – If the angles (4x + 4)° and (6x – 4)° are the supplementary angles, find the value of x.
Ans–
(4x + 4)° + (6x – 4)° = 180° (∵ Sum of the supplementary angle is 180°)
⇒ 4x + 4 + 6x – 4 = 180°
⇒ 10x = 180°
⇒ x = 18°
Thus, x = 18°
Q 45 – Find the value of y.
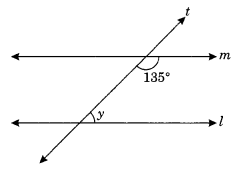
Ans–
l || m, and t is a transversal.
y + 135° = 180° (Sum of interior angles on the same side of transversal is 180°)
⇒ y = 180° – 135° = 45°
Thus, y = 45°
Q 46 – In the following figures, find the lettered angles.
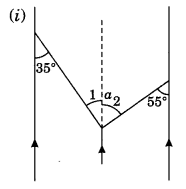
Ans–
(i) Let a be represented by ∠1 and ∠2
∠a = ∠1 + ∠2
∠1 = 35° (Alternate interior angles)
∠2 = 55° (Alternate interior angles)
∠1 + ∠2 = 35° + 55°
∠a = 90°
Thus, ∠a = 90°
Q 47 – Find the value of x.
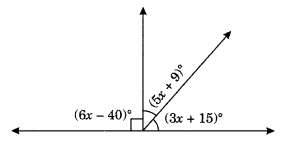
Ans–
(6x – 40)° + (5x + 9)° + (3x + 15) ° = 180° (∵ Sum of adjacent angles on straight line)
⇒ 6x – 40 + 5x + 9 + 3x + 15 = 180°
⇒ 14x – 16 = 180°
⇒ 14x = 180 + 16 = 196
⇒ x = 14
Thus, x = 14
Q 48 – In the given figure, prove that AB || CD.
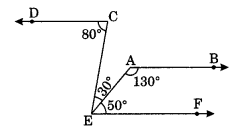
Ans–
∠CEF = 30° + 50° = 80°
∠DCE = 80° (Given)
∠CEF = ∠DCE
But these are alternate interior angle.
CD || EF ……(i)
Now ∠EAB = 130° (Given)
∠AEF = 50° (Given)
∠EAB + ∠AEF = 130° + 50° = 180°
But these are co-interior angles.
AB || EF …(ii)
From eq. (i) and (ii), we get
AB || CD || EF
Hence, AB || CD
Co-interior angles/Allied angles: Sum of interior angles on the same side of transversal is 180°.
Q 49 – In the given figure l || m. Find the values of a, b and c.
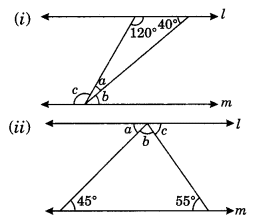
Ans–
(i) We have l || m
∠b = 40° (Alternate interior angles)
∠c = 120° (Alternate interior angles)
∠a + ∠b + ∠c = 180° (Sum of adjacent angles on straight angle)
⇒ ∠a + 40° + 120° = 180°
⇒ ∠a + 160° = 180°
⇒ ∠a = 180° – 160° = 20°
Thus, ∠a = 20°, ∠b = 40° and ∠c = 120°.
(ii) We have l || m
∠a = 45° (Alternate interior angles)
∠c = 55° (Alternate interior angles)
∠a + ∠b + ∠c = 180° (Sum of adjacent angles on straight line)
⇒ 45 + ∠b + 55 = 180°
⇒ ∠b + 100 = 180°
⇒ ∠b = 180° – 100°
⇒ ∠b = 80°
Q 50 – In the following figure, find the value of ∠BOC, if points A, O and B are collinear.
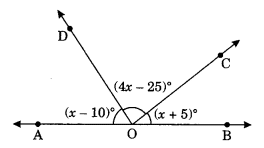
Ans–
We have A, O and B are collinear.
∠AOD + ∠DOC + ∠COB = 180° (Sum of adjacent angles on straight line)
(x – 10)° + (4x – 25)° + (x + 5)° = 180°
⇒ x – 10 + 4x – 25 + x + 5 = 180°
⇒ 6x – 10 – 25 + 5 = 180°
⇒ 6x – 30 = 180°
⇒ 6x = 180 + 30 = 210
⇒ x = 35
So, ∠BOC = (x + 5)° = (35 + 5)° = 40°
Q 51 – In the given figure, PQ, RS, and UT are parallel lines.
(i) If c = 57° and a = c / 3, find the value of d.
(ii) If c = 75° and a = 2 / 5 c , find b.
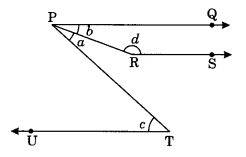
Ans–
(i) We have ∠c = 57° and ∠a = c / 3
⇒ ∠a = 19°
PQ || UT (given)
∠a + ∠b = ∠c (Alternate interior angles) for PT as transversal for Parallel Lines PQ || UT
19° + ∠b = 57°
∠b = 57° – 19° = 38°
PQ || RS (given)
∠b + ∠d = 180° (Co – interior angles)
38° + ∠d = 180°
∠d = 180° – 38° = 142°
Thus, ∠d = 142°
(ii) We have ∠c = 75° and ∠a = 2 / 5 ∠c
∠a = 2 / 5 × 75° = 30°
PQ || UT (given)
∠a + ∠b = ∠c
30° + ∠b = 75°
∠b = 75° – 30° = 45°
Thus, ∠b = 45°