Q 1 – Find the range of heights of any ten students of your class.
Ans. Let us assume heights (in cm) of 10 students of our class.
= 130, 132, 135, 137, 139, 140, 142, 143, 145, 148
By observing the above mentioned values, the highest value is = 148 cm
By observing the above mentioned values, the lowest value is = 130 cm
Then,
Range of Heights = Highest value – Lowest value
= 148 – 130
= 18 cm
Q 2 – The mode of the distribution 3,5, 7, 4, 2, 1, 4, 3, 4 is
(a) 7
(b) 4
(c) 3
(d) 1
Ans. (b) 4
Q 3 – A cricketer scores the following runs in eight innings:
58, 76, 40, 35, 46, 45, 0, 100. Find the mean score.
Ans. Mean score = (Total runs scored by the cricketer in all innings)/ (Total number of innings
Played by the cricketer)
Total runs scored by the cricketer in all innings = 58 + 76 + 40 + 35 + 46 + 45 + 0 + 100
= 400
Total number of innings = 8
Then,
Mean = (400/8)
= 50
∴Mean score of the cricketer is 50.
Q 4 – Mean of the first six prime numbers is
(a) 7.83
(b) 5.83
(c) 6.83
(d) 4.83
Ans. (c) 6.83
Q 5 – The mean of the numbers 10,20, 30 and 40 is
(a) 20
(b) 25
(c) 30
(d) 50
Ans. (b) 25
Q 6 – Find the average of the numbers 8, 13, 15.
Ans.
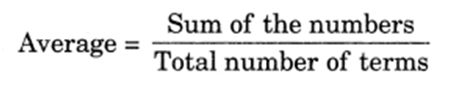
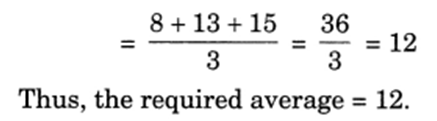
Q 7 – Find the median of the following data:
20, 14, 6, 25, 18, 13, 19, 10, 9, 12
Ans. Arranging the given data in increasing order, we get
6, 9, 10, 12, 13, 14, 18, 19, 20, 25
n = 10 (even)

Thus, the required median = 13.5
Q 8 – Anju on her birthday wants to treat her 4 friends along with herself an ice cream cone costing Rupees 17.65 each. She has only Rupees 31.45 with her. She asks her father to give her the remaining money. How much money should Anju take from her father?
Ans.
STEP-1
Cost of 1 ice-cream= Rs.17.65
Cost of 5 ice-cream= Rs. 17.65*5= Rs. 88.25
STEP-2
Cost of 5 ice-cream= Rs.88.25
Anju Had money= Rs. 31.45
She wanted more money= 88.25-31.45= Rs. 56.80
Q 9 – Find the mean of the first 5 multiples of 3.
Ans. Five multiples of 3 are 3, 6, 9, 12 and 15
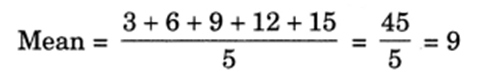
Hence, the required mean = 9.
Q 10 – Find the mean and median of first five prime numbers.
Ans. First five prime numbers are: 2, 3, 5, 7 and 11
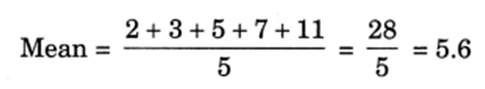
Here, n = 5
Median is the middle term, i.e., 5.
Q 11 –What is the difference between the number of tourists visiting on Friday and Monday?
(a) 10
(b) 24
(c) 38
(d) 5
Ans. (d) 5
Q 12 – A batsman scored the following number of runs in six innings:
35, 30, 45, 65, 39, 20
The mean runs scored by him in an inning is
(a) 39
(b) 38
(c) 37
(d) 40
Ans. (a) 39
Q 13 – Find the mode and median of this data. Are they same?
Ans. Arranging the given scores in an ascending order, we get
5, 9, 10, 12, 15, 16, 19, 20, 20, 20, 20, 23, 24, 25, 25
Mode,
Mode is the value of the variable which occurs most frequently.
Clearly, 20 occurs maximum number of times.
Hence, mode of the given sores is 20
Median,
The value of the middle-most observation is called the median of the data.
Here n = 15, which is odd.
Where, n is the number of the students.
∴median = value of ½ (n + 1)th observation.
= ½ (15 + 1)
= ½ (16)
= 16/2
= 8
Then, value of 8th term = 20
Hence, the median is 20.
Yes, both the values are same.
Q 14 – Find the mode and median of the data: 13, 16, 12, 14, 19, 12, 14, 13, 14
Ans. Arranging the given data in an ascending order, we get
= 12, 12, 13, 13, 14, 14, 14, 16, 19
Mode,
Mode is the value of the variable which occurs most frequently.
Clearly, 14 occurs maximum number of times.
Hence, mode of the given data is 14.
Median,
The value of the middle-most observation is called the median of the data.
Here n = 9, which is odd.
Where, n is the number of the students.
∴median = value of ½ (9 + 1)th observation.
= ½ (9 + 1)
= ½ (10)
= 10/2
= 5
Then, value of 5th term = 14
Hence, the median is 14.
Q 15 – There are 6 marbles in a box with numbers from 1 to 6 marked on each of them.
What is the probability of drawing a marble with number 2?
Ans.
From the question, it is given that
There are 6 marbles in the box with numbers from 1 to 6 are marked.
Probability of drawing a marble with number 2 = Number of favourable outcomes/
Number of possible outcomes
= (1/6)