Q 1 – Add: p2qr + pq2r + pqr2 and – 3pq2r –2pqr2
We have,
p2qr + pq2r + pqr2 + (−3pq2r−2pqr2)
= p2qr + pq2r +pqr2−3pq2r − 2pqr2
By combining the like terms,
= p2qr + pq2r − 3pq2r + pqr2−2pqr2= p2qr − 2pq2r−pqr2
Q 2 – What should be subtracted from 2x3 – 3x2y + 2xy2 + 3y3 to get x3 – 2x2y + 3xy2 + 4y3 ?
In order to get the solution, we will subtract x3−2x2y+3xy2+4y3 from 2x3−3x2y+2xy2+3y3.
Required expression is
2x3−3x2y+2xy2+3y3−(x3−2x2y+3xy2+4y3)= 2x3−3x2y+2xy2+3y3−x3+2x2y−3xy2−4y3
On combining the like terms.
=2x3−x3−3x2y+2x2y+2xy2−3xy2+3y3−4y3=x3−x2y−xy2−y3
So, if we subtract x3−x2y−xy2−y3 from 2x3−3x2y+2xy2+3y3. then we get x3−2x2y+3xy2+4y3.
Q 3 –Subtract the sum of 12ab –10b2 –18a2 and 9ab + 12b2 + 14a2 from the sum of
ab + 2b2 and 3b2 – a2
Sum of 12ab−10b2−18a2 and 9ab+12b2+14a2
=12ab−10b2−18a2+9ab+12b2+14a2
On combining the like terms,
=12ab+9ab −10b2 + 12b2−18a2+14a2 = 21ab + 2b2−4a2
Sum of ab + 2b2 and 3b2−a2
=ab+2b2+3b2−a2 = ab + 5b2−a2
Now, subtracting 21ab+2b2−4a2 from ab+5b2−a2, we get
=(ab+5b2−a2)−(21ab + 2b2 − 4a2)=ab + 5b2− a2 − 21ab − 2b2 + 4a2
On combining the like terms,
=ab −21ab + 5b2− 2b2−a2 + 4a2 = − 20ab+3b2+3a2=3a2+3b2 −20ab
Q 4 – Find the value of the following polynomials at a = – 2 and b = 3.

(a) Given expression is a2+ 2ab + b2
Substituting the given values of a and b , We get
(−2)2 + 2 (−2) (3) + (3)2
= 4 – 12 + 9 =1
Q 5 – Identify the constant terms in the following expressions:
(i) 3 + x (ii) 3 / 2 – 5y + y2 (iii) 3x2 + 2y – 1
(i) constant term = -3
(ii) constant term = 3/2
(iii) constant term = -1
Q 6 – Observe the patterns of digits made from line segments of equal length. You will find such segmented digits on the display of Computer or Mobile Phones .
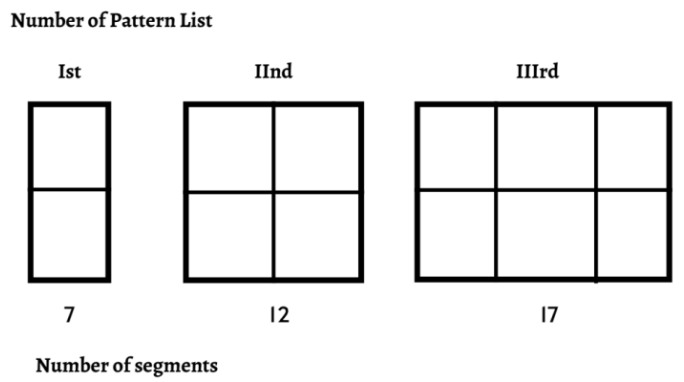
Find the rule to find the number of segments required for nth pattern. How many segments are required to form 5, 10, 100 digits of the same kind.
5n + 2
Putting n (5) = 5 5 + 2 = 27
Putting n (10) = 5 10 + 2 = 52
Putting n (100) = 5 100 + 2 = 502
Q 7 – Classify the following into monomials, binomial and trinomials.
(i) 6
(ii) 5 + x
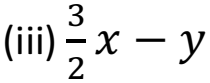
(iv) 6x2 + 5x – 3
(v) z2 + 2
The functions which have one term are called a monomial expression.
The functions which have two terms are called a binomial expressions.
Functions that have three terms are called trinomial expressions.
– 6 is monomial as it has one term.
- 5+x is binomialas it has two terms.
32x – y is binomial as it has two terms.
6x2 + 5x – 3
is trinomial as it has three terms.
Z2 + 2
is binomial as it has two terms.
Q 8 – Which one of the following is the binomial?
(a) 3xy2 + 5y –x2y
(b) x2y – 5y – x2y
(c) xy + yz + zx
(d) 3xy2 – xy2
(d) 3xy2 – xy2
Q 9 – The value of when x = 1 is
(a) 1
(b) 0
(c) 1
(d) 11
Given, the expression is 3x² – 5x + 3 .
We have to find the value of the expression when x = 1.
Put x = 1 in the expression,
3x² – 5x + 3 = 3(1)² – 5(1) + 3
= 3 – 5 + 3
= 6 – 5
= 1
Q 10 – If (x2y + y2 + 3) is subtracted from (3x2y + 2y2 + 5), then coefficient of y in the result is ________.
(a) 2x2
(b) 2
(c) 2
(d) 2y
(a) 2x2
Q 11 – How much is y4 – 12y2 + y + 14 greater than 17y3 + 34y2 – 51y + 68?
y4 -12y2 +y+14-(17y3 +34y2 -51y + 68)
= y4 -12y2 +y +14-17y3-34y2 +51y-68 On combining the like terms,
= y4-12y2-34y2 + y +51y +14- 68-17y3
= y4-46y2 + 52y-17y3 -54
= y4 -17y3 -46y2 + 52y -54
So, y4 – 12y2 + y + 14 is y4 – 17y3 – 46y2 + 52y – 54 greater than 17y3+34y2 -51y + 68
Q 12 – What should be added to 3pq + 5p2q2 + p3 to get p3 + 2p2q2 + 4pq ?
Step 1: Subtract 3pq+5p2q2+p3 from p3+2p2q2+4pq
p3+2p2q2 + 4pq −(3pq + 5p2q2 + p3) = p3 + 2p2q2 + 4pq − 3pq − 5p2q2− p3
Step 2:Combine the like terms and simplify
=(p3−p3) + (2p2q2−5p2q2)+(4pq −3pq) = > p3+2p2q2 + 4pq−(3pq+5p2q2+p3)=−3p2q2+pq
Hence, −3p2q2 + pq should be added to 3pq + 5p2q2 + p3 to get p3 + 2p2q2 + 4pq
Q 13 – Coefficient of x in – 9xy2z is
(a) 9yz
(b) 9yz
(c) –9y2z
(d) 9y2z
(c) –9y2z
Q 14 – Number of terms in the expression 3x2y – 2y2z – z2x + 5 is
(a) 2
(b) 3
(c) 4
(d) 5
(c) 4
Q 15 –Which of the following is a pair of like terms?
(a) –7xy2z, –7 x2 yz
(b) –10xyz2 , 3xyz2
(c) 3xyz , 3x2y2z2
(d) 4xyz2 , 4x2yz
(b) –10xyz2 , 3xyz2
Q 16 – Subtract 24xy – 10y – 18x from 30xy + 12y – 14x.
Step 1 of 2 :
Write down the given expressions
The given expressions are
24xy – 10y – 18x and 30xy + 12y – 14x
Step 2 of 2 :
Perform the subtraction
On subtraction we get
(30xy + 12y – 14x) – (24xy – 10y – 18x)
= 30xy + 12y – 14x –24xy + 10y + 18x
= 30xy – 24xy + 12y + 10y – 14x + 18x
= (30 – 24) xy + (12 + 10) y + (–14x + 18)x
= 6xy + 22y + 4x
Q 17 – Simplify the following expressions and then find the numerical values for x = –2.
(i) 3(2x – 4) + x2 + 5 (ii) –2(–3x + 5) – 2(x + 4)
(i) The given expression is
3(2x – 4) + x2 + 5
= 6x – 12 + x2 + 5
= x2 + 6x – 7
Which is the required simplest form
Hence the value of the expression for x = – 2
= (– 2)2 + 6× (–2) – 7
= 4 – 12 – 7
= – 15
(ii) The given expression is
= – 2(– 3x + 5) – 2(x + 4)
= 6x – 10 – 2x – 8
= 4x – 18
Which is the required simplest form
Which is the required simplest formHence the value of the expression for x = – 2
= 4 × ( – 2) – 18
= 8 – 18
= – 26
Q 18 – Rohan’s mother gave him ₹ 3xy2 and his father gave him ₹ 5(xy2 + 2). Out of this total money he spent ₹ (10 – 3xy2) on his birthday party. How much money is left with him?
It is given that rohan’s mother gave him Rs 3xy² and his father gave him Rs 5 (xy²+2) out of his money.
Total earning = 3xy2 + 5 ( xy2 + 2)
= 3xy2 + 5xy2 + 10
= 8xy2 + 10
He spent Rs(10-3xy²) on his birthday party.
Total Expenses = 10 – 3x2
We need to find the remaining amount.
Remaining amount = Total earning – Total Expenses
= 8xy2 + 10 – (10 – 3x2)
= 8xy2 + 10 – (10 – 3x2)
= 11 xy2
Q 19 – Subtract 3x2 – 5y – 2 from 5y – 3x2 + xy and find the value of the result if x = 2, y = –1.
1. To subtract : 3x² – 5y – 2
from 5y – 3x² + xy
2. Find the value of the result fot
x = 2 , y = 1
1. Here the given expressions are
3x² – 5y – 2 and 5y – 3x² + xy
On subtraction we get
= ( 5y – 3x² + xy ) – ( 3x² – 5y
– 2 )
= 5y – 3x² + xy – 3x² + 5y + 2
= – 6x² + xy + 10y + 2
2. Putting x = 2 , y = 1 we get
The required result
= – 6×2 + xy + 10y + 2
= – 6 × (2)2 (2 ×1) +
(10 × 1) + 2
= – 24 + 2 + 10 + 2
= – 10