Q 1 – If the angle between two radii of a circle is 118, then find the angle between the tangents at the ends of those radii.
GIVEN :
=> THE ANGLE BETN THE 2 RADII OF A CIRCLE WITH CENTRE O :
=> 118°
FROM FIG.
THE RADII :
=> OA AND OB
\_ AOB :
=> 118°
CONSTRUCTION :
=> DRAW TWO TANGENTS AT POINT A AND B
=> LET THEM MEET AT POINT P OUTSIDE THE CIRCLE
TO FIND :
=> \_ APB
BY THE THEOREM OF CENTRAL ANGLE :
=> THE MEASURE OF ARC CORRESPONDING TO A CENTRAL ANGLE IS EQUAL TO THE MEASURE OF THAT CENTRAL ANGLE
SO,
=> M ( ARC AB ) :
=> \_ AOB
=> 118°
MEASURE OF MAJOR ARC :
=> 360° – MEASURE OF MINOR ARC
MEASURE OF ARC AQB :
=> 360° – M ( ARC AB )
=> 360° – 118°
=> 242°
BY THE THEOREM :
=> MEASURE OF THE ANGLE MADE BY TWO TANGENTS :
=> THE CORRESPONDING MAJOR ARC – CORRESPONDING MINOR ARC / 2
\_ APB :
=> M ( AQB ) – M ( AB ) / 2
=> 242 ° – 118° / 2
=> 124° / 2
=> 62°
Q 2 – The length of the common chord of two intersecting circles is 30 cm. If the diameters of these two circles are 50 cm and 34 cm, then calculate the distance between their centers.
In △AMD, By using Pythagoras theorem AD2 = AM2 + MD2
AM2=AD2−MD2
AM2=(25)2−(15)2
AM2=400
AM=20 cm
Now in △BMD using Pythagoras BD2=DM2+MB2
MB2=BD2−DM2⇒ 172−152
MB2=64
MB=8 cm
In Distance between the center’s AB Which is ( AM + MB ) = ( 20+8 ) = 28 cm.
Q 3 – PQ and PR are tangents at Q and R, respectively. If ∠ SQR = 38, then find ∠ QPR, ∠ PRQ, ∠ QSR, and ∠ PQR.
∠SQR = 38°
∠SRQ = 38° ∵ SQ = SR = Radius
∠SQR + ∠SRQ + ∠QSR = 180° ( sum of angles of triangle )
=> 38° + 38° + ∠QSR = 180°
=> ∠QSR = 104°
∠QSR + ∠SQP + ∠SRP + ∠QPR = 360° ( sum of angles of quadrilateral )
=> 104° + 90° + 90° + ∠QPR = 360°
=> ∠QPR =76°
∠SQR = 38° ∠SQR + ∠PQR = 90° => ∠PQR =52°
∠SRQ = 38° ∠SRQ + ∠PRQ= 90° => ∠PRQ =52°
Q 4 – PA is a tangent to the circle with center O. If BC = 3 cm, AC = 4 cm, and ∆ ACB ~ ∆PAO, then find OA and OP/AP
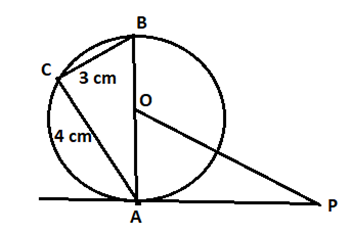
Consider the Problem
∠ACB is an angle in a semi-circle
Therefore, ∠ACB =90∘
Now, in ΔACB
We use Pythagoras’s Theorem (AB)2= (AC)2+ (BC)2
Q 5 – In the given figure, ABC is circumscribing a circle. Then, find the length of BC.
We are given the Following figure
From the figure we get,
BC = BP + PC …… (1)
Now, let us find BP and PC separately.
From the property of tangents we know that when two tangents are drawn to a circle from a common external point, the length of the two tangents from the external point to the respective points of contact will be equal. Therefore we have
BR = BP
It is given in the problem that BR = 3 cm. Therefore,
BP = 3 cm
Now let us find out PC.
Again using the same property of tangents which says that the length of two tangents drawn to a circle from the same external point will be equal, we have,
PC = QC…… (2)
From the figure we can see that,
QC = AC − AQ…… (3)
Again using the property that length of two tangents drawn to a circle from the same external point will be equal, we have,
AQ = AR
In the problem it is given that,
AR = 4 cm
Therefore,
AQ = 4 cm
Also, the length of AC is also given in the problem.
AC = 11 cm
Let us now substitute the values of AC and AQ in equation (3)
QC = 11 − 4
QC = 7
From equation (2) we can say that,
PC = 7
Finally, let us substitute the values of PC and BP in equation (1)
BC = BP + PC
BC = 3 + 7
BC = 10
Therefore, length of BC is 10 cm.
Q 6 – If a, b, and c are the sides of a right-angled triangle, where c is the hypotenuse, then prove that the radius r of the circle which touches the sides of the triangle is given by 
Let the circle touches the sides BC,CA,AB of the right triangle ABC at D,E and F respectively
where BC = a, CA = b and AB = c. then AE = AF and BD = BF Also CE = CD = r.
i.e., b – r = AF, a – r = BF
or AB = c AF + BF = b – r + a – r
This gives r = (a + b – c) 2
Q 7 – Two tangents PA and PB are drawn to the circle with centre O, such that APB = 120. Prove that OP = 2AP.
O is the center of the given circle
OAP= OBP=90
(Radius is perpendicular to the tangent at the point of contact)
OA = OB
(radius of the circle)
∴△OAP is congruent to △OBP
So that,
OP = 2AP Hence proved
Q 8 – In the given fig, AB is the diameter of a circle with center O and QC a tangent to the circle at C. If CAB = 30, then find CQA and CBA.
The radii OA, OC, and OB are of equal length.
So, angle OAC=angle OCA=30°.
Similarly, angle OBC=Angle OCB.
(i) The line CQ is the tangent, so the angle OCQ=90° as the tangent and radius are perpendicular.
Angle ACQ=Angle OCA+ angle OCQ
Angle ACQ=30°+90°
Angle ACQ=120°
Now, in ΔACQ,
Angle ACQ+ angle CAQ+ angle CQA=180°
Using values,
120°+30°+Angle CQA=180°
150°+angle CQA=180°
Angle CQA=180°-150°
Angle CQA=30°
(ii) Since AB is the diameter, angle ACB=90°. (Angle in the semi-circle)
In ΔACB,
Angle ACB+ angle CAB+ angle CBA=180°
Using values,
90°+30°+angle CBA=180°
120°+Angle CBA=180°
Angle CBA=180-120°
Angle CBA=60°
Q 9 – Prove that the angle between two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre
Draw a circle with center O and take an external point P. PA and PB are the tangents.
As the radius of the circle is perpendicular to the tangent.
OA⊥PA
Similarly OB⊥PB
OBP = 90°
OAP = 90°
In Quadrilateral OAPB, the sum of all interior angles =360
Draw a circle with center O and take an external point P. PA and PBare the tangents.
As the radius of the circle is perpendicular to the tangent.
OA⊥PA
Similarly OB⊥PB
OBP = 90°
OAP = 90°
In Quadrilateral OAPB, the sum of all interior angles =360
⇒OAP + OBP +BOA + APB = 360°
⇒90+ 90 +BOA + APB = 360°
BOA + APB =180°
⇒OAP + OBP +BOA + APB = 360°
⇒90°+ 90° +BOA + APB = 360°
BOA + APB =180°
Q 10 – Find the area of the shaded region in the given fig. where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral OAB of side 12 cm as center.
Area of Shaded region = Area of equilateral triangle ABO + Area of Major sector
= 62.352cm2
Area of Shaded region = 62.352 + 94.2 =156.55cm2
Q 11 – In the given figure, ABC is a quadrant of a circle of radius 14 cm and a semi-circle is drawn with AC as a diameter. Find the area of the shaded region.
As ABC is a quadrant of the circle, ∠BAC will be of measure 90º.
In ΔABC,
BC2 = AC2 + AB2
= (14)2 + (14)2
98cm2
=154 cm2
Area of shaded region = Area of semi-circle – (Area of sector ABDC- Area of ABC) =154 – (154 – 98) = 98cm2
Q 12 – Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q.
Ans. Step 1: Draw a circle with centre O and radius 3 cm using a compass.
Step 2: Draw a secant passing through the centre. Mark points P and Q on opposite sides of the centre at a distance of 7 cm from O.
Step 3: Place the compass on P and draw two arcs on opposite sides of OP. Now place the compass on O and draw two arcs intersecting the arcs drawn from point P.
Step 4: Join the intersection points of the arcs to obtain the perpendicular bisector of OP. Mark the mid point of OP as M1
Step 5: From M1 draw a circle with radius =M1P=M1O
Step 6: Mark the intersection points of the circle drawn from M1 with the circle drawn from O as A and B.
Step 7: Join P−A and P−B
Step 8: Repeat steps 3 to 7 for point Q and obtain tangents QC and QD
PA, PB, QC and are the required tangents.
