Introduction to Gravitation
This chapter discusses gravitation and the universal law of gravitation. The motion of objects under the influence of gravitational force on Earth is also examined closely. Students will also understand how weight varies from place to place and the conditions required for objects to float on water.
Type of forces
There are four fundamental forces in the universe and they are:
- Gravitational force
- Electromagnetic force
- Strong nuclear force
- Weak nuclear force
Gravitational Force
Gravitational force is the weakest force out of the four forces. When gravitational force is considered for massive objects, such as the sun, or giant planets, the gravitational force is considered to be strong as the masses of these objects are also large. On an atomic level, this force is considered weak.
Electromagnetic Force
Electromagnetic force is a type of physical interaction that occurs between electrically charged particles. It acts between charged particles and is a combination of magnetic and electrical forces. Electromagnetic force can be attractive or repulsive.
Strong Nuclear Force
The strong force holds together quarks, the fundamental particles that make up the protons and neutrons of the atomic nucleus, and further holds together protons and neutrons to form atomic nuclei.
Weak Nuclear Force
The weak force is the force existing between the elementary particles which are responsible for certain processes to take place at a low probability.
An object when thrown upwards, reaches a certain height and then falls downwards. (?)
We shall study how the weight of a body varies from place to place and the conditions for objects to float in liquids.
In the time of Aristotle, it was believed that an apple or any object released from a height would fall down toward the earth because it was natural for nay object to fall down towards the earth. It was thought that this fact needed no explanation because it was natural. Galileo in the 16th century suggested that since earth is attracting objects towards itself, therefore, objects fall down toward the earth.
He thought that: if the earth can attract an apple, can it not attract the moon?
Newton’s greatness lies in his ability to see that the force responsible to attract the apple made to the earth was the same force of attraction that worked between the earth and the moon or between the sun and the planets.
He argued that at each point of its orbit, the moon falls toward the earth, instead of going off in a straight line. So, it must be attracted by the earth.
But we do not really see the moon falling toward the earth
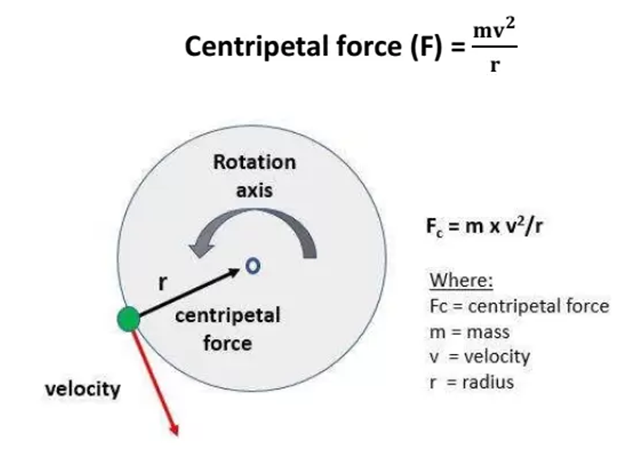
In the above diagram, a stone is moving along a circular path.
Before the thread is released, the stone moves in a circular path with a certain speed and changes direction at every point.
The change in direction involves a change in velocity or acceleration.
The force that causes this acceleration and keeps the body moving along the circular path is acting toward the center. This force is called the centripetal (meaning ‘center-seeking’) force.
In the absence of this force, the stone flies off along a straight line. This straight line will be a tangent to the circular path.
Tangent to a circle: A straight line that meets the circle at one and only one point is called a tangent to the circle. Straight line ABC is a tangent to the circle at point B. The motion of the moon around the earth is due to the centripetal force. The centripetal force is provided by the force of attraction of the earth. If there were no such force, the moon would pursue a uniform straight-line motion.
2. It is seen that a falling apple is attracted toward the earth. Does the apple attract the earth?
Ans. Yes , but we do not see the earth moving toward an apple.
According to the third law of motion, the apple does attract the earth But according to the second law of motion, for a given force,
( F is constant , FA=FE )
The mass of an apple is negligibly small compared to that of the earth. So, we do not see the earth moving towards the apple. Extend the same argument for why the earth does not move towards the moon.
Newton concluded that not only does the earth attract an apple and the moon, but all objects in the universe attract each other.
This force of attraction between objects is called the gravitational force.
Gravitational force: it is the force of attraction between any two objects in the universe by the virtue of their masses.
What is Gravitation?
Gravitation or just gravity is the force of attraction between any two bodies. All the objects in the universe attract each other with a certain amount of force, but in most cases, the force is too weak to be observed due to the very large distance of separation. Besides, gravity’s range is infinite but the effect becomes weaker as objects move away.
Some examples of gravity are:
- The force that causes the ball to come down is known as gravity
- Gravity keeps the planets in orbit around the sun.
- Gravity is the force that causes a rock to roll downhill.
Gravitational Force
Gravitational force is the weakest force out of the four forces. When gravitational force is considered for massive objects, such as the sun, or giant planets, the gravitational force is considered to be strong as the masses of these objects are also large. On an atomic level, this force is considered weak.
The Universal Law of Gravitation
Every object in the universe attracts every other object in the universe with a force of attraction, called gravitation, which is :
- directly proportional to the product of masses of the objects.
- inversely proportional to the square of the distance between them.
- acts along the line joining the centers of both objects.
This is called Newton’s Law of Gravitation or the Universal Law of Gravitation. Suppose there are two objects having mass ‘M’ and ‘m’ respectively The distance between their centers is equal to ‘d’. The force of attraction is F.
The force is along the line joining the centers of two objects.

∴ From Law of Gravitation states that the force of attraction by which an object attracts other
another object is directly proportional to the product of their masses.
The Law of Gravitation also states that the force of attraction by which an object attracts another object is inversely proportional to the square of the distance between them.
G is called a universal constant because its value does not depend on the nature of the intervening medium or temperature or any other physical variable.
S.I. unit of G = Nm2/kg2
Value of G = 6.673 x 10-11 Nm2/kg2 (Found by Henry Cavendish)
This Law is applicable everywhere in the universe, thus it is known as the UNIVERSAL LAW OF
GRAVITATION
GRAVITATIONAL CONSTANT: is equal to the gravitational force acting between two bodies, each of mass 1 kg and kept at a distance of 1m from each other. If m1= m2= 1 kg and d = 1m
Value of G = 6.67 × 10-11Nm2 kg-2
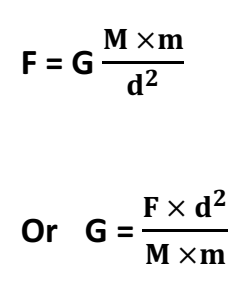
GRAVITATIONAL CONSTANT: is equal to the gravitational force acting between two bodies, each of mass 1 kg and kept at a distance of 1m from each other.
If m1= m2= 1 kg d = 1m
The universal gravitational constant is numerically equal to the gravitational force of attraction between two objects of masses 1kg each and placed at a distance of 1 m from their centres.
The value of ‘G’ was found out by Henry Cavendish, a British philosopher and scientist.
SOME IMPORTANT POINTS REGARDING GRAVITATIONAL FORCE OF ATTRACTION:
(a)The gravitational force of attraction does not change with the change in the medium between the
point masses. (air or water)
(b) The force applied by one object on the second is always equal to the force applied by the second on first.
This means the Newton’s law of gravitation obeys Newton’s third law.
(c) It is the weakest force of attraction in nature. (G = 6.67 × 10-11 Nm2kg-2 )
(d) It is always attractive in nature.
(e) It obeys inverse square law. F ∝ 1/d2
(f) It is a long- range force. It is also applicable between the galaxies.
IMPORTANCE OF THE UNIVERSAL LAW OF GRAVITATION:
The universal law of gravitation successfully explained several phenomena which were believed to be
unconnected:
(a) the force that binds us to the earth.
(b) the motion of the moon around the earth.
(c) the motion of planets around the Sun.
(d) the tides due to the moon and the Sun.
(e) holding the atmosphere near the surface of the earth.
Applications of Newton’s law of gravitation:
(a) Determination of the masses of planets and stars: Using the relation, the mass of the heavenly body (M) =gr2/G
(a) Estimating the masses of the double stars: a double star is a system of stars consisting two stars orbiting round their common center of mass. From the extent of irregularity in the motion of a star due to the gravitational pull by some other star bound to it, can be used for estimating their masses. Such a small irregularity in motion is called wobble.
If the distance between the two objects is doubled , What will be the new gravitational force?
Ans. Then the gravitational force becomes one-fourth of the original force.
When the distance is ‘R’ then FO∝ 1/R2
When the distance becomes 2R, then FN∝1/(2R)2
From these two relationships, we can write Fn/Fo = 1/(2R)2 × R2/1 = 1/4
If the distance between two objects is halved, what will be the new gravitational force?
Then the new gravitational force becomes four times of the original force.
When the distance is ‘d’ then
When the distance becomes d/2, then
From these two relationships, we can write
Since we know that FO =
Given, the distance between their centers becomes halved new distance = d/2
New gravitational Force FN =
FN = 4. FO
All objects when dropped from a certain height fall towards the earth.
The gravitational force of the earth on the earth is caused by it. If you drop a cotton ball and a stone from a certain height simultaneously, which of the two will fall first? Obviously, you will say stone as it is heavier than a cotton ball.
Conclusion: Heavier objects fall faster than lighter objects.
Galileo showed that all objects whether heavy or light, fall at the same speed toward the earth.
“If there were no air, all the bodies having different masses when dropped simultaneously from the same height would hit the ground at the same time.”
The motion of a body towards the earth when no other force except the force of gravity acts on it is called a free fall.
Thus all freely falling bodies irrespective of their mass fall towards the earth with the same acceleration.
Though he was not able to prove it experimentally, Robert Boyle proved it experimentally. He placed a coin and a feather in a long glass tube and removed its air with the help of a vacuum pump.
When he inverted the glass tube, he observed that the both coin and feather fell to the bottom of the glass tube at the same time.
He proved that acceleration produced in all the freely falling bodies is the same and it does not depend on the mass of the falling body.
Relation between Newton’s third law of motion and Newton’s law of gravitation
- According to Newton’s third law of motion, “Every object exerts equal and opposite force against another object but in opposite direction.”
- According to Newton’s law of gravitation, “Every mass in the universe attracts every other ”
- In the case of freely falling stone and earth, the stone is attracted toward earth means earth attracts the stone.
- But according to Newton’s third law of motion, the stone should also attract the earth.
- It is true that stone also attracts the earth with the same force F = m × a but due to the very less mass of the stone, the acceleration (a) in its velocity is 9.8 m/s2, and acceleration (a) of earth towards stone is 1.65 × 10 –24 m/s2 which is negligible and we cannot feel it.
Importance of universal law of gravitation
The universal law of gravitation successfully explained several phenomena like :
- the force that binds us to the earth.
- the motion of the moon around the earth.
- the motion of planets around the sun.
- the tides due to the moon and the sun.
- holding the atmosphere near the surface of the earth.
F ∝ M × g
EXPRESSION FOR ACCELERATION DUE TO GRAVITY (g):
Let mass of the object put under free fall = m
And acceleration due to gravity = g
Therefore, according to Newton’s Second Law of Motion which states that Force is the product of mass and acceleration,
F = m × g —————–(i)
Now, according to the Universal Law of gravitation,
Thus from the above two expressions (i) and (ii), we get
Where ‘g’ is the acceleration due to gravity,
‘G’ is the Universal Gravitational Constant.
‘Me’ is the mass of the earth.
And ‘Re’ is the distance between the object and the center of the earth.
Since we know that
Where, ‘g’ is acceleration due to gravity,
‘G’ is the Universal Gravitational Constant.
‘Me’ is the mass of earth.
And ‘Re’ is the distance between object and center of earth.
(a) the value of ‘g’ does not depend upon the mass or distance of an object falling on the earth/ planet.
Therefore, all objects (of different masses) fall over the earth at the same rate.
(b) It depends on the radius and mass of the earth /planet.
VARIATION IN VALUE OF ‘g’ ON THE EARTH:
The acceleration due to gravity at a place changes due to the following effects:
(a) The effect of the shape of the earth
(b) The effect of rotational motion of the earth
(c) The effect of height or altitude
(d) The effect of depth
THE EFFECT OF SHAPE OF THE EARTH:
The acceleration due to gravity(g) on the surface of the earth is given by:
Since, earth is not a perfect sphere rather it has oblique shape. Therefore, radius at the equator is
greater than at the poles.
Since we know that value of ‘g’ is reciprocal of the square of radius of earth,
Thus, the value of ‘g’ will be greater at the poles and less at the equator.
Or gp > ge
And the value of ‘g’ will decrease with the increase in distance of the object from the center of the earth.
THE EFFECT OF THE ROTATIONAL MOTION OF THE EARTH:
The rotation of the earth also causes variation in acceleration due to gravity (g).
The variation in this case also depends on the latitude of a place.
The value of ‘g’ is maximum at the poles and minimum at the equator. Thus due to the rotation of the earth too, the weight of an object is maximum at the poles and minimum at the equator.
THE EFFECT OF HEIGHT FROM THE SURFACE OF THE EARTH:
Let g be the value of acceleration due to gravity at a point P on the surface of the earth.
Therefore,
Let g’ be the acceleration due to gravity at height ‘h’ above the surface of the earth at point Q.
Therefore,
Dividing equation (ii) by equation (i), we have
Dividing equation (ii) by equation (i), we have
Since ‘R’ < (R + h)
Therefore g’ > g
Acceleration due to gravity decreases by going higher from the surface of the earth.
THE EFFECT OF DEPTH:
This equation shows that value of ‘g’ should increase on going down inside the earth because then, the value of ‘Re’ decreases. This ,however, is not true. Actually this formula is not applicable at any point inside the earth. It has been found that the value of ‘g’ decreases as we go down inside the earth.
The value of ‘g’ at a depth ‘d’ below the surface of the earth is given by :
At the centre of the earth d= Re
therefore value of ‘g’ at the center of the earth= 0
CALCULATION OF VALUE OF ‘g’:
To calculate the value of ‘g’ we should know the values of ‘G ,mass of the earth (Me), and the radius of the earth(Re).
Therefore, after substituting the value of G, Me, and Re in the expression for ‘g’ we get the value of the acceleration of gravity (g).
The value of acceleration of gravity (g) = 9.8 m/s2
HOW DOES GRAVITY (g) DIFFER FROM GRAVTATION (G):
Since we know that the gravitational force is the force of attraction between any two objects by virtue of their masses.
Gravity is the force of attraction exerted by a huge heavenly body such as, the earth, the moon or the sun etc., on a smaller object near its surface. It does not depend on the mass of the falling body.
The earth pulls an object of mass 1kg towards it with a force of 9.8N. so, 9.8N is the gravity of the earth.
From this we find that gravity is a particular case of gravitation.
The Moon’s Falling – Moon’s revolution around Earth
The moon revolves around the Earth due to centripetal force, which is the force of gravity of the Earth. If the force of attraction between the Earth and the moon ceases, then the moon will continue to travel in a straight line path tangential to its orbit around the Earth.
Freefall
When an object falls down towards the earth under the gravitational force alone, we say the object is in free fall.
The velocity of a freely falling body changes and is said to be accelerated.
This acceleration is called acceleration due to gravity, denoted by ’g’. Unit is m/s2.
EQUATIONS OF MOTION UNDER THE INFLUENCE OF THE GRAVITY:
The equations for motion are as follows:
These equations of motion are also applied to calculate the Velocity, Height, by replacing ‘a’ by ‘g’. After substituting ‘g’ in the place of ‘a’ we get above equations as follows:
When an object is falling under the influence of the gravity:
When an object is thrown up against gravity:
MASS: It is defined as the quantity of matter present in a body. Mass is expressed in the mass unit.
It is denoted ‘m’. S.I unit of mass is the kilogram (Kg).
Characteristic of mass:
(a) It is a scalar quantity.
(b) Mass of a body remains the same at all places.
(c) The mass of an object is measured with the help of a beam balance.
(d) It can never be zero.
WEIGHT:
The weight of a body on the earth is the force with which the earth attracts the body towards its
centre.
Weight of the body= force of gravity
We know that force of gravity acting on the body = Mass of the body × acceleration due to gravity
∴ Weight of a body= Mass of the body × Acceleration due to gravity
W= m × g
S.I unit of weight is newton (N).
W= m × g
Since the value of ‘g’ is always constant at a given place,
Weight of a body of mass 1 kg ?
Weight = Mass of the body × Acceleration due to gravity
= m × g
= 1 kg × 9.8 m/s2
W= 9.8 N ( N= kg × m/s2)
A body of mass 1 kg on the surface of the earth weighs= 9.8 N
In common use we express weight of an object in kilogram-weight (kg-wt) or gram-weight(g-wt)
units.
kilogram-weight (kg-wt) and gram-weight(g-wt) are gravitational units of weight.
1kg-wt = 1 kg × g = 1 kg × 9.8 m/s2 (F= m × g)
1kg-wt = 9.8 N
9.8 N is the gravitational force which acts on an object of mass 1 kg.
CHACTERISTICS OF WEIGHT:
(a) Weight is a vector quantity because it has magnitude and its direction is always towards the
centre of the earth.
(b) Weight is measured with the help of a spring balance or on a weighing machine.
(c) Weight of a body is directly proportional to its mass at a given place.
(d) Weight of a body changes with the value of ‘g’.
(e) Weight of all the bodies becomes zero at the centre of the earth.
WEIGHT OF A BODY ON THE MOON:
Since we know that the weight of a body on the earth’s surface is the force with which it is attracted by the earth towards its centre.
Where Me is the mass of the earth and Re is the radius of the earth.
Similarly weight of the body on the surface of moon :
Where Mm is the mass of the earth and Rm is the radius of the earth. On dividing Wm by We
since we know that mass of the earth is about 100 times that of the moon and the radius of the earth is 4 times that of the moon .
Me = 100 Mm
Re = 4 Rm
weight of an object on the moon is one –sixth of the weight of the object on the earth.
Introduction to Kepler’s Laws
Motion is always relative. Based on the energy of the particle under motion, the motions are classified into two types:
- Bounded Motion
- Unbounded Motion
In bounded motion, the particle has negative total energy (E<0) and has two or more extreme points where the total energy is always equal to the potential energy of the particle i.e the kinetic energy of the particle becomes zero.
For eccentricity 0≤ e <1, E<0 implies the body has bounded motion. A circular orbit has eccentricity e = 0 an elliptical orbit has eccentricity e < 1.
In unbounded motion, the particle has positive total energy (E>0) and has a single extreme point where the total energy is always equal to the potential energy of the particle i.e the kinetic energy of the particle becomes zero.
For eccentricity e ≥ 1, E > 0 implies the body has unbounded motion. Parabolic orbit has eccentricity e = 1 and Hyperbolic path has eccentricity e>1
Kepler’s First law – The Law of Orbits
According to Kepler’s first law,” All the planets revolve around the sun in elliptical orbits having the sun at one of the foci”. The point at which the planet is close to the sun is known as perihelion and the point at which the planet is farther from the sun is known as aphelion.
It is the characteristic of an ellipse that the sum of the distances of any planet from two foci is constant. The elliptical orbit of a planet is responsible for the occurrence of seasons.
Kepler’s Second Law – The Law of Equal Areas
Kepler’s second law states ” The radius vector drawn from the sun to the planet sweeps out equal areas in equal intervals of time”
As the orbit is not circular, the planet’s kinetic energy is not constant in its path. It has more kinetic energy near the perihelion and less kinetic energy near the aphelion implying more speed at the perihelion and less speed (vmin) at the aphelion. If r is the distance of planet from sun, at perihelion (rmin) and at aphelion (rmax), then,
rmin + rmax = 2a × (length of major axis of an ellipse) . . . . . . . (1)
Kepler’s Second Law – The law of Equal Areas
Using the law of conservation of angular momentum the law can be verified. At any point of time, the angular momentum can be given as, L = mr2ω.
Now consider a small area ΔA described in a small time interval Δt and the covered angle is Δθ. Let the radius of curvature of the path be r, then the length of the arc covered = r Δθ.
Now, by conservation of angular momentum, L is a constant
Thus, dA/dt = constant
The area swept in equal intervals of time is a constant.
Kepler’s second law can also be stated as “The areal velocity of a planet revolving around the sun in elliptical orbit remains constant which implies the angular momentum of a planet remains constant”. As the angular momentum is constant all planetary motions are planar motions, which is a direct consequence of central force.
Kepler’s Third Law – The Law of Periods
According to Kepler’s law of periods,” The square of the time period of revolution of a planet around the sun in an elliptical orbit is directly proportional to the cube of its semi-major axis”.
Shorter the orbit of the planet around the sun, the shorter the time taken to complete one revolution. Using the equations of Newton’s law of gravitation and laws of motion, Kepler’s third law takes a more general form:
P2 = 4π2 /[G(M1+ M2)] × a3
Thrust and Pressure
Force acting on an object perpendicular to the surface is called thrust. The effect of thrust depends on the area of contact. The pressure is thrust per unit area. SI unit is the pascal (Pa). Force acting on a smaller area applies more pressure than the same force acting on a larger area.
Pressure in fluids
The pressure exerted by a fluid in a container is transmitted undiminished in all directions on the walls of the container.
Archimedes’ Principle – Why objects float or sink
The upward force exerted by a fluid on an object is known as upthrust or buoyant force.
The magnitude of buoyancy depends on the density of the fluid. If the density of an object is less than the fluid, it will float. If the density of the object is greater than the fluid, it will sink.
According to Archimedes’ principle, when a body is immersed fully or partially in a fluid, it experiences an upward force that is equal to the weight of the fluid displaced by it.
Buoyancy
It is often observed that while swimming our body feels light or while taking out water from the well, the bucket feels lighter when it is partially or fully immersed in water. The reason behind this is that our body experiences forces from the downward direction or the opposite direction of the gravitational pull. This results in a decrease in weight. This is one of the reasons why the plastic balls float on the water instead of sinking in the water due to their weight.
The upward force exerted by a fluid opposes the weight of an object, immersed in the fluid. The pressure at the bottom of an object submerged in the fluid is always greater than at the top. The difference in the pressure of the fluid results in the net upward force on the object. This upward force is termed Buoyancy. It is necessary to understand density and relativity to completely understand the concept of Buoyancy.
Applications of Buoyancy
It is due to buoyancy that human swimmers, fish, ships, and icebergs stay afloat. Some applications of buoyancy are given in the points below.
Submarine
Buoyancy makes it possible for swimmers, fishes, ships, and icebergs to stay afloat. Some of the prominent applications of buoyancy are given below:
Ship
A ship floats on the surface of the sea because the volume of water displaced by the ship is enough to have a weight equal to the weight of the ship. A ship is constructed in a way so that the shape is hollow, to make the overall density of the ship lesser than the seawater. Therefore, the buoyant force acting on the ship is large enough to support its weight.
Fish
A certain group of fishes uses Archimedes’ principle to go up and down the water. To go up to the surface, the fish will fill its swim bladder (air sacs) with gases (clever isn’t it?). The gases diffuse from their own body to the bladder and thus makes the body lighter. This enables the fish to go up.
Buoyant Force
The buoyant force is the upward force exerted on an object wholly or partly immersed in a fluid. This upward force is also called Upthrust. Due to the buoyant force, a body submerged partially or fully in a fluid appears to lose its weight, i.e. appears to be lighter.
The following factors affect buoyant force:
- the density of the fluid
- the volume of the fluid displaced
- the local acceleration due to gravity
An object whose density is greater than that of the fluid in which it is submerged tends to sink. If the object is either less dense than the liquid or is shaped appropriately (as in a boat), the force can keep the object afloat. In terms of relative density, if the relative density is less than one, it floats in water and substances with a relative density greater than one sink in water.
What causes Buoyant Force?
When an object is immersed in water or any other fluid, we observe that the object experiences a force from the downward direction opposite to the gravitational pull, which is responsible for the decrease in its weight. This upward force exerted by the fluid opposes the weight of an object immersed in a fluid. As we know, the pressure in a fluid column increases with depth. Thus, the pressure at the bottom of an object submerged in the fluid is greater than that at the top. The difference in this pressure results in a net upward force on the object which we define as buoyancy.
When we submerge an object in a fluid, an upward force is experienced by the object. The fluid applies this force on the object, which causes it to rise, and we call this force buoyant force. The magnitude of this force is precisely equal to the amount of weight of the liquid displaced.
The point where the buoyant force is applied or the point on the object where the force acts is termed the Center of Buoyancy.
When we submerge an object in a fluid, an upward force is experienced by the object. The fluid applies this force on the object, which causes it to rise, and we call this force buoyant force. The magnitude of this force is precisely equal to the amount of weight of the liquid displaced.
The point where the buoyant force is applied or the point on the object where the force acts is termed the Center of Buoyancy.
Archimedes’ Principle
The upward buoyant force that is exerted on a body immersed in a fluid, whether partially or fully submerged, is equal to the weight of the fluid that the body displaces and acts in the upward direction at the center of mass of the displaced fluid”.
The value of thrust force is given by the Archimedes law which Archimedes of Syracuse of Greece discovered. When an object is partially or fully immersed in a liquid, the apparent loss of weight is equal to the weight of the liquid displaced by it.
Archimedes’ Principle Explanation
If you look at the figure, the weight due to gravity is opposed by the thrust provided by the fluid. The object inside the liquid only feels the total force acting on it as the weight. Because the actual gravitational force is decreased by the liquid’s upthrust, the object feels as though its weight is reduced. The apparent weight is thus given by:
Apparent weight= Weight of object (in the air) – Thrust force (buoyancy)
Archimedes’ principle tells us that the weight loss is equal to the weight of liquid the object displaces
Archimedes’ Principle Formula
In simple form, Archimedes’ law states that the buoyant force on an object is equal to the weight of the fluid displaced by the object. Mathematically written as:
Fb = ρ x g x V
Where Fb is the buoyant force, ρ is the density of the fluid, V is the submerged volume, and g is the acceleration due to gravity.
Archimedes’ Principle Derivation
We know that density is defined as
Archimedes’ Principle Experiment
- Take a container filled with water to the brim.
- Now take any solid object you like and measure its weight using a spring balance. Note this down.
- Keep the object attached to the spring balance and submerge it in the water. Just make sure the spring balance is not submerged.
- Now, note down the weight shown by the spring balance. You will notice that it is less. Some water will be displaced into the bowl.
- Collect this water and weigh it. You will find that the weight of the water will be exactly equal to the loss of weight of the object!
Archimedes’ Principle Applications
Following are the applications of Archimedes’ principle:
Submarine:
The reason why submarines are always underwater is that they have a component called a ballast tank which allows the water to enter making the submarine be in its position underwater as the weight of the submarine is greater than the buoyant force.
Hot-air balloon:
The reason why hot-air balloons rise and float in mid-air is that the buoyant force of the hot-air balloon is less than the surrounding air. When the buoyant force of the hot-air balloon is more, it starts to descend. This is done by varying the quantity of hot air in the balloon.
Hydrometer:
A hydrometer is an instrument used for measuring the relative density of liquids. Hydrometer consists of lead shots which makes them float vertically on the liquid. The lower the hydrometer sinks, the lesser is the density of the liquid.`
Why does an object float or sink in water?
If one considers a single column of liquid, then it can be viewed as a concoction of the many overlying layers, one over the other, with fluctuating pressure. The pressure at the bottom of the liquid would be greater than at the top; this is because as we go down in the liquid, the number of layers of the liquid that are overlying, i.e. the layers one over the other, increases.
Owing to the difference in the pressure amid the layers, there tends to be a made-up force being applied to it in the upward direction. This force leads to the acceleration of the object that has been submerged in the upward direction. The force is always in the vertical direction.
It can also be said that the magnitude of the upward force is equivalent to the difference in the pressure of the topmost and the last layer and equivalent to the weight of the fluid displaced.
Floating is the consequence of the above concept. The object should be less dense than water, or else, if its density is greater, it will tend to sink.
Density
The mass per unit volume of material is termed as Density. The density is used to measure how tightly packed the matter is.
Density ρ = Mass/Volume = M / V
Introduction to Gravitation
This chapter discusses gravitation and the universal law of gravitation. The motion of objects under the influence of gravitational force on Earth is also examined closely. Students will also understand how weight varies from place to place and the conditions required for objects to float on water.
Type of forces
There are four fundamental forces in the universe and they are:
- Gravitational force
- Electromagnetic force
- Strong nuclear force
- Weak nuclear force
Gravitational Force
Gravitational force is the weakest force out of the four forces. When gravitational force is considered for massive objects, such as the sun, or giant planets, the gravitational force is considered to be strong as the masses of these objects are also large. On an atomic level, this force is considered weak.
Electromagnetic Force
Electromagnetic force is a type of physical interaction that occurs between electrically charged particles. It acts between charged particles and is a combination of magnetic and electrical forces. Electromagnetic force can be attractive or repulsive.
Strong Nuclear Force
The strong force holds together quarks, the fundamental particles that make up the protons and neutrons of the atomic nucleus, and further holds together protons and neutrons to form atomic nuclei.
Weak Nuclear Force
The weak force is the force existing between the elementary particles which are responsible for certain processes to take place at a low probability.
An object when thrown upwards, reaches a certain height and then falls downwards. (?)
We shall study how the weight of a body varies from place to place and the conditions for objects to float in liquids.
In the time of Aristotle, it was believed that an apple or any object released from a height would fall down toward the earth because it was natural for nay object to fall down towards the earth. It was thought that this fact needed no explanation because it was natural. Galileo in the 16th century suggested that since earth is attracting objects towards itself, therefore, objects fall down toward the earth.
He thought that: if the earth can attract an apple, can it not attract the moon?
Newton’s greatness lies in his ability to see that the force responsible to attract the apple made to the earth was the same force of attraction that worked between the earth and the moon or between the sun and the planets.
He argued that at each point of its orbit, the moon falls toward the earth, instead of going off in a straight line. So, it must be attracted by the earth.
But we do not really see the moon falling toward the earth

In the above diagram, a stone is moving along a circular path.
Before the thread is released, the stone moves in a circular path with a certain speed and changes direction at every point.
The change in direction involves a change in velocity or acceleration.
The force that causes this acceleration and keeps the body moving along the circular path is acting toward the center. This force is called the centripetal (meaning ‘center-seeking’) force.
In the absence of this force, the stone flies off along a straight line. This straight line will be a tangent to the circular path.
Tangent to a circle: A straight line that meets the circle at one and only one point is called a tangent to the circle. Straight line ABC is a tangent to the circle at point B. The motion of the moon around the earth is due to the centripetal force. The centripetal force is provided by the force of attraction of the earth. If there were no such force, the moon would pursue a uniform straight-line motion.
2. It is seen that a falling apple is attracted toward the earth. Does the apple attract the earth?
Ans. Yes , but we do not see the earth moving toward an apple.
According to the third law of motion, the apple does attract the earth But according to the second law of motion, for a given force,
( F is constant , FA=FE )
The mass of an apple is negligibly small compared to that of the earth. So, we do not see the earth moving towards the apple. Extend the same argument for why the earth does not move towards the moon.
Newton concluded that not only does the earth attract an apple and the moon, but all objects in the universe attract each other.
This force of attraction between objects is called the gravitational force.
Gravitational force: it is the force of attraction between any two objects in the universe by the virtue of their masses.
What is Gravitation?
Gravitation or just gravity is the force of attraction between any two bodies. All the objects in the universe attract each other with a certain amount of force, but in most cases, the force is too weak to be observed due to the very large distance of separation. Besides, gravity’s range is infinite but the effect becomes weaker as objects move away.
Some examples of gravity are:
- The force that causes the ball to come down is known as gravity
- Gravity keeps the planets in orbit around the sun.
- Gravity is the force that causes a rock to roll downhill.
Gravitational Force
Gravitational force is the weakest force out of the four forces. When gravitational force is considered for massive objects, such as the sun, or giant planets, the gravitational force is considered to be strong as the masses of these objects are also large. On an atomic level, this force is considered weak.
The Universal Law of Gravitation
Every object in the universe attracts every other object in the universe with a force of attraction, called gravitation, which is :
- directly proportional to the product of masses of the objects.
- inversely proportional to the square of the distance between them.
- acts along the line joining the centers of both objects.
This is called Newton’s Law of Gravitation or the Universal Law of Gravitation. Suppose there are two objects having mass ‘M’ and ‘m’ respectively The distance between their centers is equal to ‘d’. The force of attraction is F.
The force is along the line joining the centers of two objects.

∴ From Law of Gravitation states that the force of attraction by which an object attracts other
another object is directly proportional to the product of their masses.
The Law of Gravitation also states that the force of attraction by which an object attracts another object is inversely proportional to the square of the distance between them.
G is called a universal constant because its value does not depend on the nature of the intervening medium or temperature or any other physical variable.
S.I. unit of G = Nm2/kg2
Value of G = 6.673 x 10-11 Nm2/kg2 (Found by Henry Cavendish)
This Law is applicable everywhere in the universe, thus it is known as the UNIVERSAL LAW OF
GRAVITATION
GRAVITATIONAL CONSTANT: is equal to the gravitational force acting between two bodies, each of mass 1 kg and kept at a distance of 1m from each other. If m1= m2= 1 kg and d = 1m
Value of G = 6.67 × 10-11Nm2 kg-2
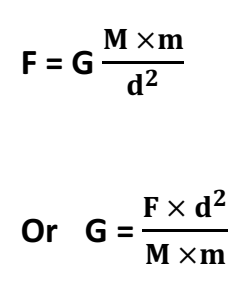
GRAVITATIONAL CONSTANT: is equal to the gravitational force acting between two bodies, each of mass 1 kg and kept at a distance of 1m from each other.
If m1= m2= 1 kg d = 1m
The universal gravitational constant is numerically equal to the gravitational force of attraction between two objects of masses 1kg each and placed at a distance of 1 m from their centres.
The value of ‘G’ was found out by Henry Cavendish, a British philosopher and scientist.
SOME IMPORTANT POINTS REGARDING GRAVITATIONAL FORCE OF ATTRACTION:
(a)The gravitational force of attraction does not change with the change in the medium between the
point masses. (air or water)
(b) The force applied by one object on the second is always equal to the force applied by the second on first.
This means the Newton’s law of gravitation obeys Newton’s third law.
(c) It is the weakest force of attraction in nature. (G = 6.67 × 10-11 Nm2kg-2 )
(d) It is always attractive in nature.
(e) It obeys inverse square law. F ∝ 1/d2
(f) It is a long- range force. It is also applicable between the galaxies.
IMPORTANCE OF THE UNIVERSAL LAW OF GRAVITATION:
The universal law of gravitation successfully explained several phenomena which were believed to be
unconnected:
(a) the force that binds us to the earth.
(b) the motion of the moon around the earth.
(c) the motion of planets around the Sun.
(d) the tides due to the moon and the Sun.
(e) holding the atmosphere near the surface of the earth.
Applications of Newton’s law of gravitation:
(a) Determination of the masses of planets and stars: Using the relation, the mass of the heavenly body (M) =gr2/G
(a) Estimating the masses of the double stars: a double star is a system of stars consisting two stars orbiting round their common center of mass. From the extent of irregularity in the motion of a star due to the gravitational pull by some other star bound to it, can be used for estimating their masses. Such a small irregularity in motion is called wobble.
If the distance between the two objects is doubled , What will be the new gravitational force?
Ans. Then the gravitational force becomes one-fourth of the original force.
When the distance is ‘R’ then FO∝ 1/R2
When the distance becomes 2R, then FN∝1/(2R)2
From these two relationships, we can write Fn/Fo = 1/(2R)2 × R2/1 = 1/4
If the distance between two objects is halved, what will be the new gravitational force?
Then the new gravitational force becomes four times of the original force.
When the distance is ‘d’ then
When the distance becomes d/2, then
From these two relationships, we can write
Since we know that FO =
Given, the distance between their centers becomes halved new distance = d/2
New gravitational Force FN =
FN = 4. FO
All objects when dropped from a certain height fall towards the earth.
The gravitational force of the earth on the earth is caused by it. If you drop a cotton ball and a stone from a certain height simultaneously, which of the two will fall first? Obviously, you will say stone as it is heavier than a cotton ball.
Conclusion: Heavier objects fall faster than lighter objects.
Galileo showed that all objects whether heavy or light, fall at the same speed toward the earth.
“If there were no air, all the bodies having different masses when dropped simultaneously from the same height would hit the ground at the same time.”
The motion of a body towards the earth when no other force except the force of gravity acts on it is called a free fall.
Thus all freely falling bodies irrespective of their mass fall towards the earth with the same acceleration.
Though he was not able to prove it experimentally, Robert Boyle proved it experimentally. He placed a coin and a feather in a long glass tube and removed its air with the help of a vacuum pump.
When he inverted the glass tube, he observed that the both coin and feather fell to the bottom of the glass tube at the same time.
He proved that acceleration produced in all the freely falling bodies is the same and it does not depend on the mass of the falling body.
Relation between Newton’s third law of motion and Newton’s law of gravitation
- According to Newton’s third law of motion, “Every object exerts equal and opposite force against another object but in opposite direction.”
- According to Newton’s law of gravitation, “Every mass in the universe attracts every other ”
- In the case of freely falling stone and earth, the stone is attracted toward earth means earth attracts the stone.
- But according to Newton’s third law of motion, the stone should also attract the earth.
- It is true that stone also attracts the earth with the same force F = m × a but due to the very less mass of the stone, the acceleration (a) in its velocity is 9.8 m/s2, and acceleration (a) of earth towards stone is 1.65 × 10 –24 m/s2 which is negligible and we cannot feel it.
Importance of universal law of gravitation
The universal law of gravitation successfully explained several phenomena like :
- the force that binds us to the earth.
- the motion of the moon around the earth.
- the motion of planets around the sun.
- the tides due to the moon and the sun.
- holding the atmosphere near the surface of the earth.
F ∝ M × g
EXPRESSION FOR ACCELERATION DUE TO GRAVITY (g):
Let mass of the object put under free fall = m
And acceleration due to gravity = g
Therefore, according to Newton’s Second Law of Motion which states that Force is the product of mass and acceleration,
F = m × g —————–(i)
Now, according to the Universal Law of gravitation,
Thus from the above two expressions (i) and (ii), we get
Where ‘g’ is the acceleration due to gravity,
‘G’ is the Universal Gravitational Constant.
‘Me’ is the mass of the earth.
And ‘Re’ is the distance between the object and the center of the earth.
Since we know that
Where, ‘g’ is acceleration due to gravity,
‘G’ is the Universal Gravitational Constant.
‘Me’ is the mass of earth.
And ‘Re’ is the distance between object and center of earth.
(a) the value of ‘g’ does not depend upon the mass or distance of an object falling on the earth/ planet.
Therefore, all objects (of different masses) fall over the earth at the same rate.
(b) It depends on the radius and mass of the earth /planet.
VARIATION IN VALUE OF ‘g’ ON THE EARTH:
The acceleration due to gravity at a place changes due to the following effects:
(a) The effect of the shape of the earth
(b) The effect of rotational motion of the earth
(c) The effect of height or altitude
(d) The effect of depth
THE EFFECT OF SHAPE OF THE EARTH:
The acceleration due to gravity(g) on the surface of the earth is given by:
Since, earth is not a perfect sphere rather it has oblique shape. Therefore, radius at the equator is
greater than at the poles.
Since we know that value of ‘g’ is reciprocal of the square of radius of earth,
Thus, the value of ‘g’ will be greater at the poles and less at the equator.
Or gp > ge
And the value of ‘g’ will decrease with the increase in distance of the object from the center of the earth.
THE EFFECT OF THE ROTATIONAL MOTION OF THE EARTH:
The rotation of the earth also causes variation in acceleration due to gravity (g).
The variation in this case also depends on the latitude of a place.
The value of ‘g’ is maximum at the poles and minimum at the equator. Thus due to the rotation of the earth too, the weight of an object is maximum at the poles and minimum at the equator.
THE EFFECT OF HEIGHT FROM THE SURFACE OF THE EARTH:
Let g be the value of acceleration due to gravity at a point P on the surface of the earth.
Therefore,
Let g’ be the acceleration due to gravity at height ‘h’ above the surface of the earth at point Q.
Therefore,
Dividing equation (ii) by equation (i), we have
Dividing equation (ii) by equation (i), we have
Since ‘R’ < (R + h)
Therefore g’ > g
Acceleration due to gravity decreases by going higher from the surface of the earth.
THE EFFECT OF DEPTH:
This equation shows that value of ‘g’ should increase on going down inside the earth because then, the value of ‘Re’ decreases. This ,however, is not true. Actually this formula is not applicable at any point inside the earth. It has been found that the value of ‘g’ decreases as we go down inside the earth.
The value of ‘g’ at a depth ‘d’ below the surface of the earth is given by :
At the centre of the earth d= Re
therefore value of ‘g’ at the center of the earth= 0
CALCULATION OF VALUE OF ‘g’:
To calculate the value of ‘g’ we should know the values of ‘G ,mass of the earth (Me), and the radius of the earth(Re).
Therefore, after substituting the value of G, Me, and Re in the expression for ‘g’ we get the value of the acceleration of gravity (g).
The value of acceleration of gravity (g) = 9.8 m/s2
HOW DOES GRAVITY (g) DIFFER FROM GRAVTATION (G):
Since we know that the gravitational force is the force of attraction between any two objects by virtue of their masses.
Gravity is the force of attraction exerted by a huge heavenly body such as, the earth, the moon or the sun etc., on a smaller object near its surface. It does not depend on the mass of the falling body.
The earth pulls an object of mass 1kg towards it with a force of 9.8N. so, 9.8N is the gravity of the earth.
From this we find that gravity is a particular case of gravitation.
The Moon’s Falling – Moon’s revolution around Earth
The moon revolves around the Earth due to centripetal force, which is the force of gravity of the Earth. If the force of attraction between the Earth and the moon ceases, then the moon will continue to travel in a straight line path tangential to its orbit around the Earth.
Freefall
When an object falls down towards the earth under the gravitational force alone, we say the object is in free fall.
The velocity of a freely falling body changes and is said to be accelerated.
This acceleration is called acceleration due to gravity, denoted by ’g’. Unit is m/s2.
EQUATIONS OF MOTION UNDER THE INFLUENCE OF THE GRAVITY:
The equations for motion are as follows:
These equations of motion are also applied to calculate the Velocity, Height, by replacing ‘a’ by ‘g’. After substituting ‘g’ in the place of ‘a’ we get above equations as follows:
When an object is falling under the influence of the gravity:
When an object is thrown up against gravity:
MASS: It is defined as the quantity of matter present in a body. Mass is expressed in the mass unit.
It is denoted ‘m’. S.I unit of mass is the kilogram (Kg).
Characteristic of mass:
(a) It is a scalar quantity.
(b) Mass of a body remains the same at all places.
(c) The mass of an object is measured with the help of a beam balance.
(d) It can never be zero.
WEIGHT:
The weight of a body on the earth is the force with which the earth attracts the body towards its
centre.
Weight of the body= force of gravity
We know that force of gravity acting on the body = Mass of the body × acceleration due to gravity
∴ Weight of a body= Mass of the body × Acceleration due to gravity
W= m × g
S.I unit of weight is newton (N).
W= m × g
Since the value of ‘g’ is always constant at a given place,
Weight of a body of mass 1 kg ?
Weight = Mass of the body × Acceleration due to gravity
= m × g
= 1 kg × 9.8 m/s2
W= 9.8 N ( N= kg × m/s2)
A body of mass 1 kg on the surface of the earth weighs= 9.8 N
In common use we express weight of an object in kilogram-weight (kg-wt) or gram-weight(g-wt)
units.
kilogram-weight (kg-wt) and gram-weight(g-wt) are gravitational units of weight.
1kg-wt = 1 kg × g = 1 kg × 9.8 m/s2 (F= m × g)
1kg-wt = 9.8 N
9.8 N is the gravitational force which acts on an object of mass 1 kg.
CHACTERISTICS OF WEIGHT:
(a) Weight is a vector quantity because it has magnitude and its direction is always towards the
centre of the earth.
(b) Weight is measured with the help of a spring balance or on a weighing machine.
(c) Weight of a body is directly proportional to its mass at a given place.
(d) Weight of a body changes with the value of ‘g’.
(e) Weight of all the bodies becomes zero at the centre of the earth.
WEIGHT OF A BODY ON THE MOON:
Since we know that the weight of a body on the earth’s surface is the force with which it is attracted by the earth towards its centre.
Where Me is the mass of the earth and Re is the radius of the earth.
Similarly weight of the body on the surface of moon :
Where Mm is the mass of the earth and Rm is the radius of the earth. On dividing Wm by We
since we know that mass of the earth is about 100 times that of the moon and the radius of the earth is 4 times that of the moon .
Me = 100 Mm
Re = 4 Rm
weight of an object on the moon is one –sixth of the weight of the object on the earth.
Introduction to Kepler’s Laws
Motion is always relative. Based on the energy of the particle under motion, the motions are classified into two types:
- Bounded Motion
- Unbounded Motion
In bounded motion, the particle has negative total energy (E<0) and has two or more extreme points where the total energy is always equal to the potential energy of the particle i.e the kinetic energy of the particle becomes zero.
For eccentricity 0≤ e <1, E<0 implies the body has bounded motion. A circular orbit has eccentricity e = 0 an elliptical orbit has eccentricity e < 1.
In unbounded motion, the particle has positive total energy (E>0) and has a single extreme point where the total energy is always equal to the potential energy of the particle i.e the kinetic energy of the particle becomes zero.
For eccentricity e ≥ 1, E > 0 implies the body has unbounded motion. Parabolic orbit has eccentricity e = 1 and Hyperbolic path has eccentricity e>1
Kepler’s First law – The Law of Orbits
According to Kepler’s first law,” All the planets revolve around the sun in elliptical orbits having the sun at one of the foci”. The point at which the planet is close to the sun is known as perihelion and the point at which the planet is farther from the sun is known as aphelion.
It is the characteristic of an ellipse that the sum of the distances of any planet from two foci is constant. The elliptical orbit of a planet is responsible for the occurrence of seasons.
Kepler’s Second Law – The Law of Equal Areas
Kepler’s second law states ” The radius vector drawn from the sun to the planet sweeps out equal areas in equal intervals of time”
As the orbit is not circular, the planet’s kinetic energy is not constant in its path. It has more kinetic energy near the perihelion and less kinetic energy near the aphelion implying more speed at the perihelion and less speed (vmin) at the aphelion. If r is the distance of planet from sun, at perihelion (rmin) and at aphelion (rmax), then,
rmin + rmax = 2a × (length of major axis of an ellipse) . . . . . . . (1)
Kepler’s Second Law – The law of Equal Areas
Using the law of conservation of angular momentum the law can be verified. At any point of time, the angular momentum can be given as, L = mr2ω.
Now consider a small area ΔA described in a small time interval Δt and the covered angle is Δθ. Let the radius of curvature of the path be r, then the length of the arc covered = r Δθ.
Now, by conservation of angular momentum, L is a constant
Thus, dA/dt = constant
The area swept in equal intervals of time is a constant.
Kepler’s second law can also be stated as “The areal velocity of a planet revolving around the sun in elliptical orbit remains constant which implies the angular momentum of a planet remains constant”. As the angular momentum is constant all planetary motions are planar motions, which is a direct consequence of central force.
Kepler’s Third Law – The Law of Periods
According to Kepler’s law of periods,” The square of the time period of revolution of a planet around the sun in an elliptical orbit is directly proportional to the cube of its semi-major axis”.
Shorter the orbit of the planet around the sun, the shorter the time taken to complete one revolution. Using the equations of Newton’s law of gravitation and laws of motion, Kepler’s third law takes a more general form:
P2 = 4π2 /[G(M1+ M2)] × a3
Thrust and Pressure
Force acting on an object perpendicular to the surface is called thrust. The effect of thrust depends on the area of contact. The pressure is thrust per unit area. SI unit is the pascal (Pa). Force acting on a smaller area applies more pressure than the same force acting on a larger area.
Pressure in fluids
The pressure exerted by a fluid in a container is transmitted undiminished in all directions on the walls of the container.
Archimedes’ Principle – Why objects float or sink
The upward force exerted by a fluid on an object is known as upthrust or buoyant force.
The magnitude of buoyancy depends on the density of the fluid. If the density of an object is less than the fluid, it will float. If the density of the object is greater than the fluid, it will sink.
According to Archimedes’ principle, when a body is immersed fully or partially in a fluid, it experiences an upward force that is equal to the weight of the fluid displaced by it.
Buoyancy
It is often observed that while swimming our body feels light or while taking out water from the well, the bucket feels lighter when it is partially or fully immersed in water. The reason behind this is that our body experiences forces from the downward direction or the opposite direction of the gravitational pull. This results in a decrease in weight. This is one of the reasons why the plastic balls float on the water instead of sinking in the water due to their weight.
The upward force exerted by a fluid opposes the weight of an object, immersed in the fluid. The pressure at the bottom of an object submerged in the fluid is always greater than at the top. The difference in the pressure of the fluid results in the net upward force on the object. This upward force is termed Buoyancy. It is necessary to understand density and relativity to completely understand the concept of Buoyancy.
Applications of Buoyancy
It is due to buoyancy that human swimmers, fish, ships, and icebergs stay afloat. Some applications of buoyancy are given in the points below.
Submarine
Buoyancy makes it possible for swimmers, fishes, ships, and icebergs to stay afloat. Some of the prominent applications of buoyancy are given below:
Ship
A ship floats on the surface of the sea because the volume of water displaced by the ship is enough to have a weight equal to the weight of the ship. A ship is constructed in a way so that the shape is hollow, to make the overall density of the ship lesser than the seawater. Therefore, the buoyant force acting on the ship is large enough to support its weight.
Fish
A certain group of fishes uses Archimedes’ principle to go up and down the water. To go up to the surface, the fish will fill its swim bladder (air sacs) with gases (clever isn’t it?). The gases diffuse from their own body to the bladder and thus makes the body lighter. This enables the fish to go up.
Buoyant Force
The buoyant force is the upward force exerted on an object wholly or partly immersed in a fluid. This upward force is also called Upthrust. Due to the buoyant force, a body submerged partially or fully in a fluid appears to lose its weight, i.e. appears to be lighter.
The following factors affect buoyant force:
- the density of the fluid
- the volume of the fluid displaced
- the local acceleration due to gravity
An object whose density is greater than that of the fluid in which it is submerged tends to sink. If the object is either less dense than the liquid or is shaped appropriately (as in a boat), the force can keep the object afloat. In terms of relative density, if the relative density is less than one, it floats in water and substances with a relative density greater than one sink in water.
What causes Buoyant Force?
When an object is immersed in water or any other fluid, we observe that the object experiences a force from the downward direction opposite to the gravitational pull, which is responsible for the decrease in its weight. This upward force exerted by the fluid opposes the weight of an object immersed in a fluid. As we know, the pressure in a fluid column increases with depth. Thus, the pressure at the bottom of an object submerged in the fluid is greater than that at the top. The difference in this pressure results in a net upward force on the object which we define as buoyancy.
When we submerge an object in a fluid, an upward force is experienced by the object. The fluid applies this force on the object, which causes it to rise, and we call this force buoyant force. The magnitude of this force is precisely equal to the amount of weight of the liquid displaced.
The point where the buoyant force is applied or the point on the object where the force acts is termed the Center of Buoyancy.
When we submerge an object in a fluid, an upward force is experienced by the object. The fluid applies this force on the object, which causes it to rise, and we call this force buoyant force. The magnitude of this force is precisely equal to the amount of weight of the liquid displaced.
The point where the buoyant force is applied or the point on the object where the force acts is termed the Center of Buoyancy.
Archimedes’ Principle
The upward buoyant force that is exerted on a body immersed in a fluid, whether partially or fully submerged, is equal to the weight of the fluid that the body displaces and acts in the upward direction at the center of mass of the displaced fluid”.
The value of thrust force is given by the Archimedes law which Archimedes of Syracuse of Greece discovered. When an object is partially or fully immersed in a liquid, the apparent loss of weight is equal to the weight of the liquid displaced by it.
Archimedes’ Principle Explanation
If you look at the figure, the weight due to gravity is opposed by the thrust provided by the fluid. The object inside the liquid only feels the total force acting on it as the weight. Because the actual gravitational force is decreased by the liquid’s upthrust, the object feels as though its weight is reduced. The apparent weight is thus given by:
Apparent weight= Weight of object (in the air) – Thrust force (buoyancy)
Archimedes’ principle tells us that the weight loss is equal to the weight of liquid the object displaces
Archimedes’ Principle Formula
In simple form, Archimedes’ law states that the buoyant force on an object is equal to the weight of the fluid displaced by the object. Mathematically written as:
Fb = ρ x g x V
Where Fb is the buoyant force, ρ is the density of the fluid, V is the submerged volume, and g is the acceleration due to gravity.
Archimedes’ Principle Derivation
We know that density is defined as
Archimedes’ Principle Experiment
- Take a container filled with water to the brim.
- Now take any solid object you like and measure its weight using a spring balance. Note this down.
- Keep the object attached to the spring balance and submerge it in the water. Just make sure the spring balance is not submerged.
- Now, note down the weight shown by the spring balance. You will notice that it is less. Some water will be displaced into the bowl.
- Collect this water and weigh it. You will find that the weight of the water will be exactly equal to the loss of weight of the object!
Archimedes’ Principle Applications
Following are the applications of Archimedes’ principle:
Submarine:
The reason why submarines are always underwater is that they have a component called a ballast tank which allows the water to enter making the submarine be in its position underwater as the weight of the submarine is greater than the buoyant force.
Hot-air balloon:
The reason why hot-air balloons rise and float in mid-air is that the buoyant force of the hot-air balloon is less than the surrounding air. When the buoyant force of the hot-air balloon is more, it starts to descend. This is done by varying the quantity of hot air in the balloon.
Hydrometer:
A hydrometer is an instrument used for measuring the relative density of liquids. Hydrometer consists of lead shots which makes them float vertically on the liquid. The lower the hydrometer sinks, the lesser is the density of the liquid.`
Why does an object float or sink in water?
If one considers a single column of liquid, then it can be viewed as a concoction of the many overlying layers, one over the other, with fluctuating pressure. The pressure at the bottom of the liquid would be greater than at the top; this is because as we go down in the liquid, the number of layers of the liquid that are overlying, i.e. the layers one over the other, increases.
Owing to the difference in the pressure amid the layers, there tends to be a made-up force being applied to it in the upward direction. This force leads to the acceleration of the object that has been submerged in the upward direction. The force is always in the vertical direction.
It can also be said that the magnitude of the upward force is equivalent to the difference in the pressure of the topmost and the last layer and equivalent to the weight of the fluid displaced.
Floating is the consequence of the above concept. The object should be less dense than water, or else, if its density is greater, it will tend to sink.
Density
The mass per unit volume of material is termed as Density. The density is used to measure how tightly packed the matter is.
Density ρ = Mass/Volume = M / V