Q 1 – Graphically, the pair of equations 7x – y = 5; 21x – 3y = 10 represents two lines which are
(a) intersecting at one point
(b) parallel
(c) intersecting at two points
(d) coincident
(b) parallel
Q 2 – The pair of equations 3x – 5y = 7 and – 6x + 10y = 7 have
(a) a unique solution
(b) infinitely many solutions
(c) no solution
(d) two solutions
(c) no solution
Q 3 – The pair of equation x = – 4 and y = – 5 graphically represents lines which are
(a) intersecting at (– 5, – 4)
(b) intersecting at (– 4, – 5)
(c) intersecting at (5, 4)
(d) intersecting at (4, 5)
(b) intersecting at (– 4, – 5)
Q 4 – The graph of x = -2 is a line parallel to the
(a) x-axis
(b) y-axis
(c) both x- and y-axis
(d) none of these
(b) y-axis
Q 5 – Two equations in two variables taken together are called
(a) linear equations
(b) quadratic equations
(c) simultaneous equations
(d) none of these
(c) simultaneous equations
Q 6 – x and y are 2 different digits. If the sum of the two digit numbers formed by using both the digits is a perfect square, then value of x+ y is (Sample)
(a) 10
(b) 11
(c) 12
(d) 13
(b) 11
Q 7 – The father’s age is six times his son’s age. Four years hence, the age of the father will be four times his son’s age. The present ages (in year) of the son and the father are, respectively.
(a) 4 and 24
(b) 5 and 30
(c) 6 and 36
(d) 3 and 24
(c) 6 and 36
Q 8 – Half the perimeter of a rectangular garden, whose length is 4m more than its width is 36m. Find the dimensions of the garden.
Let the width of the garden =x meter
Then length=(x+4) meter
Half perimeter =36 m
So perimeter of garden =(2×36)=72 meters
According to the question
⇒2(l+b)=72
⇒2(x+x+4)=72
⇒2x+2x+4=74⇒4x=64⇒x=16 meters
Hence,the width of the garden =16 meters
The length of the garden =(16+4)=20 meters
Q 9 – The sum of two positive numbers is 100 and the difference between their squares is 1000. Find the numbers
then x²+y²=100
x²-y²=28
2x²=128
x²=64 x=8 as x is positive
y²=100–64=36,y=6
Thus sum of numbers x+y=8+6=14
Q 10 – Draw the graphs of the equations x – y + 1 = 0 and 3x + 2y – 12 = 0. Determine the coordinates of the triangle formed by these lines and the x axis. Also shade the triangular region.
Ans. By plotting the graph of two linear equations and x-axis, a triangle can be formed and shaded and hence, the vertices can be located.
x – y + 1 = 0
⇒ y = x + 1
x | -1 | 2 |
y = x + 1 | 0 | 3 |
3x + 2y -12 = 0
⇒ 2y = 12 – 3x
⇒ y = (12 – 3x) / 2
x | 4 | 2 |
y = (12 – 3x) / 2 | 0 | 3 |

Q 11 – A and B are two points 150 km apart on a highway. Two cars start from A and B at the same time. If they move in the same direction, they meet in 15 hours. But if they move in the opposite direction, they meet in one hour. Find their speed
Ans. Let the speed of Car which starts from A be x km per hour
And the speed of the Car which starts from B be y km per hour
Then according to the question
When cars move in the same direction till 15 Hour . then,
Distance covered by the car at A− distance covered by the car at B =150km
i.e.,15x−15y=150 …………………….1
Also according to the question when the car moves in the opposite direction till 1 Hour. Then,
Distance covered by the car at A = distance covered by the car at B =150km
i.e.,1x+1y=150 ……………….2
Solving eq. 1 and 2 we get,
x=80 km per hour
and ,y=70 km per hour
Q 12 – A train covered a certain distance at a uniform speed. If the train would have been 6 km/hr. faster, it would have taken 4 hours less than the scheduled time and if the train were slower by 6km/ hr., it would have taken 6 hours more than the scheduled time. Find the distance of the journey.
Let x km/hr be the speed of train
Let y be the time taken by the train
Distance = speed x time
= x y
To form the first equation let us consider the given information from the question that is If the train had been 6 km/hr faster,it would have taken 4 hours less than the scheduled time.
it clearly says that speed is increased by 6 and time is reduced by 4
So , (x + 6) (y – 4) = x y
x y – 4 x + 6 y – 24 = x y
x y – x y – 4 x + 6 y = 24
– 4 x + 6 y = 24
divided by (-2) => 2 x – 3 y = -12 —– (1)
To form the second equation let us consider the given information from the question that is If the train were slower by 6km/hr, then it would have taken 6 hours more than the scheduled time.
it clearly says that speed is reduced by 6 and time is increased by 6
So , (x – 6) (y + 6) = x y
x y + 6 x – 6 y – 36 = x y
x y – x y + 6 x – 6 y = 36
6 x – 6 y = 36
divided by (6) => x – y = 6 —– (2)
2 x – 3 y = -12
(2) x 2 => 2 x – 2 y = 12
(-) (+) (-)
—————
– y = -24
y = 24
Now we have to apply the value of y in the first equation to get value of x
Substitute y = 24 in the first equation we get
2 x – 3 (24) = -12
2 x – 72 = -12
2 x = -12 + 72
2 x = 60
x = 60/2
x = 30
Speed of the train = 30 km/hr
Time taken by the train = 24 hours
Distance covered by the train = x y = 30 x 24 = 720 km
Verification:
2 x – 3 y = -12
2(30) – 3(24) = -12
60 – 72 = -12
-12 = -12
Q 13 – On comparing the ratios a1/a2, b1/b2, and c1/c2, find out whether the following pair of linear equations are consistent, or inconsistent.
(i) 3x + 2y = 5 ; 2x – 3y = 7
(ii) 2x – 3y = 8 ; 4x – 6y = 9
(i) Given : 3x + 2y = 5 or 3x + 2y – 5 = 0
and 2x – 3y = 7 or 2x – 3y – 7 = 0
Comparing the above equations with a1x + b1y + c1=0
And a2x + b2y + c2 = 0
We get,
a1 = 3, b1 = 2, c1 = -5
a2 = 2, b2 = -3, c2 = -7
a1/a2 = 3/2, b1/b2 = 2/-3, c1/c2 = -5/-7 = 5/7
Since, a1/a2≠b1/b2 the lines intersect each other at a point and have only one possible solution.
Hence, the equations are consistent.
(ii) Given 2x – 3y = 8 and 4x – 6y = 9
Therefore,
a1 = 2, b1 = -3, c1 = -8
a2 = 4, b2 = -6, c2 = -9
a1/a2 = 2/4 = 1/2, b1/b2 = -3/-6 = 1/2, c1/c2 = -8/-9 = 8/9
Since, a1/a2=b1/b2≠c1/c2
Q 14 – The coach of a cricket team buys 7 bats and 6 balls for Rs.3800. Later, she buys 3 bats and 5 balls for Rs.1750. Find the cost of each bat and each ball.
Let the cost of a bat be x and the cost of a ball be y.
According to the question,
7x + 6y = 3800 ………………. (i)
3x + 5y = 1750 ………………. (ii)
From (i), we get;
y = (3800 – 7x)/6 …………………… (iii)
Substituting (iii) in (ii). we get,
3x + 5[(3800 – 7x)/6] = 1750
⇒3x + (9500/3) – (35x/6) = 1750
3x – (35x/6) = 1750 – (9500/3)
(18x – 35x)/6 = (5250 – 9500)/3
⇒-17x/6 = -4250/3
⇒-17x = -8500
x = 500
Putting the value of x in (iii), we get;
y = (3800 – 7 × 500)/6 = 300/6 = 50
Hence, the cost of a bat is Rs 500 and the cost of a ball is Rs 50.
Q 15 – Solve the following pair of linear equations by the substitution and cross-multiplication methods:
8x + 5y = 9
3x + 2y = 4
8x + 5y = 9 …………………..(1)
3x + 2y = 4 ……………….….(2)
From equation (2) we get;
x = (4 – 2y) / 3 ……………………. (3)
Substituting this value in equation 1, we get
8[(4 – 2y)/3] + 5y = 9
32 – 16y + 15y = 27
-y = -5
y = 5 ……………………………….(4)
Substituting this value in equation (2), we get
3x + 10 = 4
3x = -6
x = -2
Thus, x = -2 and y = 5.
Now, Using Cross Multiplication method:
8x +5y – 9 = 0
3x + 2y – 4 = 0
x/(-20 + 18) = y/(-27 + 32 ) = 1/(16 – 15)
-x/2 = y/5 = 1/1
∴ x = -2 and y =5.
Q 16 – Solve each of the following pair of linear equations by elimination method:
Q 17 – Solve the equations x + 2y – 4 = 0 and 2x + 4y – 12 = 0 graphically.
Given,
x + 2y – 4 = 0….(i)
2x + 4y – 12 = 0….(ii)
From (i),
x + 2y = 4
2y = 4 – x
y = (4 – x)/2
x | 0 | 2 | 4 |
y | 4 | 1 | 0 |
From (ii),
2x + 4y = 12
x + 2y = 6
2y = 6 – x
y = (6 – x)/2
x | 0 | 2 | 4 |
y | 3 | 2 | 1 |
Here, the lines represent the given pair of linear equations are parallel.
Thus, there is no solution to the given pair of linear equations.
Q 18 – In ∆ABC, LA = x, ∠B = 3x, and ∠C = y if 3y – 5x = 30°, show that triangle is right angled.
∠A + 2B + ∠C = 180°
(Sum of interior angles of A ABC) x + 3x + y = 180°
4x + y = 180° …(i)
3y – 5x = 30° (Given) …(ii) Multiply equation (i) by 3 and subtracting from eq. (ii), we get
-17x = – 510 = x = 910 = 30°
17 then _A = x = 30° and 2B = 3x = 3 X 30o = 90°
∠C = y = 180° – (∠A + ∠B) = 180° – 120° = 60°
∠A = 30°, ∠B = 90°, ∠C = 60° Hence ∆ABC is right triangle right angled at B.
Q 19 – ABCDE is a pentagon with BE|CD and BC||DE. BC is perpendicular to CD. If the perimeter of ABCDE is 21 cm. Find the value of x and y.
Since BC||DE and BE||CD with BC||CD.
BCDE is a rectangle.
Opposite sides are equal BE = CD
∴ x + y = 5 …… (i)
DE = BC = x – y
Since perimeter of ABCDE is 21 cm.
AB + BC + CD + DE + EA = 21
3 + x – y + x + y + x – y + 3 = 21 ⇒ 6 + 3x – y = 21
3x – y = 15 ….. (iii)
Adding (i) and (ii), we get
4x = 20 ⇒ x = 5
On putting the value of x in (i), we get y = 0
Hence, x = 5 and y = 0.
Q 20 – Five years ago, A was thrice as old as B and ten years later, A shall be twice as old as B. What are the present ages of A and B?
Let the present ages of B and A be x years and y years respectively. Then
B’s age 5 years ago = (x – 5) years
and A’s age 5 years ago = (- 5) years
(-5) = 3 (x – 5) = 3x – y = 10 …….(i)
B’s age 10 years hence = (x + 10) years
A’s age 10 years hence = (y + 10) years
y + 10 = 2 (x + 10) = 2x – y = -10 …….. (ii)
On subtracting (ii) from (i) we get x = 20
Putting x = 20 in (i) we get
(3 × 20) – y = 10 ⇒ y = 50
∴ x = 20 and y = 50
Hence, B’s present age = 20 years and A’s present age = 50 years.
Q 21 – Draw the graph of the equations x – y + 1 = 0 and 3x + 2y – 12 = 0. Determine the coordinates of the vertices of the triangle formed by these lines and the x-axis, and shade the triangular region.
We have,’ x – y + 1 = 0 and 3x + 2y – 12 = 0
Thus, x – y = -1 => x = y – 1 …(i)
3x + 2y = 12 => x = 12−2y/3 12−2y3 … (ii)
From equation (ii), we have
Plotting this, we have
ABC is the required (shaded) region and point of intersection is (2, 3).
∴ The vertices of the triangle are (-1, 0), (4, 0), (2, 3).
Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method
Q 22 – Solve each of the following pair of linear equations by cross multiplication method:
a. 11x + 15y + 23 = 0, 7x – 2y – 20 = 0
b. ax + by = – a, bx + ay = – b
Q 23 – Solve : 99x + 101y = 499, 101x + 99 y = 501
Given equation are
99x + 101y = 499−−−(1)
101x + 99y = 501−−−(2)
Adding (1) and (2)
200x + 200y=1000
∴ x + y = 5−−−(3)
Subtracting (1) from (2)
2x−2y=2
∴ x−y=1−−−(4)
Adding (3) and (4)
2x = 6 ∴ x = 3
Putting x=3 in equation (4)
3 − y = 1 ∴ y = 2
∴ y = 2,x = 3
Q 24 – Determine the values of m and n so that the following system of linear equation have infinite number of solutions :
(2m – 1)x + 3y – 5 = 0
3x + (n – 1)y – 2 = 0
(2m-1)x + 3y – 5 = 0
3x + (n-1)y – 2 = 0
There are infinite number of solutions
So , a1/a2 = b1/b2 = c1/c2
(2m-1) / 3 = 3 / (n-1) = 5/2
Equating 1 and 2
We have 4m – 2 = 15
4m = 17
m = 17/4
Equating 2 and 3
We have 5n – 5 = 6
5n = 11
n = 11/5
Q 25 – Solve the following pair of equations for x and y:
first equation
Q 26 – The cost of 2 kg of apples and 1kg of grapes on a day was found to be Rs. 160. After a month, the cost of 4kg of apples and 2kg of grapes is Rs. 300. Represent the situations algebraically and geometrically.
let us consider that price of apple be x & grapes be y
case1:
2x+y=160 …………..eq1
case 2:
4x+2y=300 …………………..eq2
divide equation 2 on both side by 2
2x+y=150 …………………………eq 3
we got two equations 1&3
2x+y=160 &2x+y=150
then put simanteniously x and y values
in eq 1 in eq 3
2x+y=160 2x+y=150
x=50 x=50
100+y=160 100+y=150
y=60 y=50
x=30 x=30
60+y=160 60+y=150
y=100 y=90
then mark this point on graph and you will find that both the lines will be parallel to each other
Q 27 – For what values of a and b does the following pair of linear equations have infinite number of solution ?
2x + 3y = 7, a (x + y) – b (x – y) = 3a + b – 2
2x -3y = 7……….(1)
ax + 3y = b ………….(2)
On comparing with General form of a pair of linear equations in two variables x & y is:
a1x + b1y + c1 = 0
and a2x + b2y + c2= 0
a1= 2 , b1= – 3, c1= – 7
a2= a, b2= 3 , c2= – b
a1/a2= 2/a , b1/b2= -3/3, c1/c2= -7/-b = 7/b
Given: A pair of linear equations has a infinite solution, if
a1/a2 = b1/b2 = c1/c2
2/a = -3/3 = 7/b
I II III
Taking the first two terms
2/a = -3/3
-3a = 2× 3
-3a = 6
a = -6/3
a= -2
Taking the II and III terms
-3/3 = 7/b
-1 = 7/b
-b = 7
b = -7
Hence, the value of a = -2 & b= -7
Q 28 – Solve each of the following pair of linear equations by substitution method:
a) 3x + 2y – 5 = 0; 6x – 5 y – 1 = 0
b) 5x + 8y = 9; 2x + 3y = 4
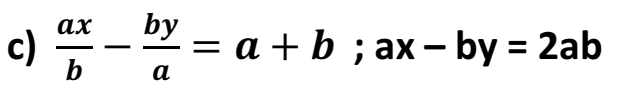
Q 29 – Half the perimeter of a rectangular garden, whose length is 4 m more than its width is 36 m. Find the dimensions of the garden.
Let be the length of the rectangular garden and be the width.
Now, According to the question, the length is 4 m more than its width .i.e.
l = b + 4
l–b=4 …………(1)
Also Given Half Parameter of the rectangle = 36 i.e.
l + b =36 ……..(2)
Now, as we have two equations, on adding both equations, we get,
l + b + l – b = 4 + 36
⇒2l = 40
⇒ l = 20
Putting this in equation (1),
⇒ 20 – b = 4
⇒b = 20 – 4
⇒b = 16
Hence Length and width of the rectangle are 20m and 16 respectively.
Q 30 – Solve each of the following pair of linear equations graphically:
a) 3x + 2y = 8; 4x – 5y = 3
b) 3x + 5y – 12 = 0; 3x –5y + 18 = 0
For eq “3x + 2y= 8”
Graphical representation is
A(2,1) B(4,-2) C(6,-4)
And for eq.” 4x-5y=3″
Graphical representation is
A(2,1) B(7,5) C(12,9)
Step-by-step explanation:
We need to put the value on the place of x and y
to get the value given on R. H.S.
Like
3x + 2y = 8
Let x is 2 and y is 1
Put values
3 (2) + 2 (1) = 8
6 + 2 = 8
L.H.S.= R.H.S.
3 x+ 5y = 12
⇒ 3x = 12 − 5y
The table for 3x + 5y = 12 is
x | 4 | –1 | – 6 |
y | 0 | 3 | – 1 |
Also we have 3x − 5y + 18 = 0
⇒ 3x = 5y −18
The table for 3x − 5y +18 = 0 is
x | – 6 | – 4 | – 1 |
y | 0 | 6 | 3 |
Q 31 – Draw the graphs of the equations x – y + 1 = 0 and 3x + 2y – 12 = 0. Determine the coordinates of the triangle formed by these lines and the x axis. Also shade the triangular region.
Given, the equations for graphs are x – y + 1 = 0 and 3x + 2y – 12 = 0.
For, x – y + 1 = 0 or x = 1+y
x | 0 | 1 | 2 |
y | 1 | 2 | 3 |
For, 3x + 2y – 12 = 0 or x = (12-2y)/3
x | 4 | 2 | 0 |
y | 0 | 3 | 6 |
The graphical represnetaion of the equations are
Q 32 – The sum of two positive numbers is 100 and the difference between their squares is 1000. Find the numbers.
Then x²+y²=100
x²-y² =28
2x² =128
x²= 64 x = 8 as x is positive
y² = 100 – 64 = 36,y = 6
Thus sum of numbers x + y = 8 + 6 = 14
Q 33 – Draw the graph of the following equations: 2x + y = 2 ; 2y – x =4 What is the area of the triangle formed by the two lines and the line y = 0?
2x+y=2
2y-x=4
y = 0
2x+y=2 , y = 0
=> point of intersection ( 1 , 0)
2y-x=4 , y = 0
=> point of intersection ( -4 , 0)
2x+y=2 , 2y-x=4
=> point of intersection ( 0 , 2)
Triangle is formed with base = ( 1 – (-4) = 5
Height = 2
Area of Triangle = (1/2) * base * height
= (1/2) * 5 * 2
= 5 sq units
or area of triangles by vertex ( 1 , 0) , ( -4 , 0) and ( 0 , 2)
= (1/2) | 1 ( 0 – 2) – 4( 2 – 0) + 0 (0 – 0) |
= (1/2) | – 2 – 8 |
= (1/2) | – 10 |
= (1/2) (10)
= 5 sq units
Q 34 – The sum of digits of two digit number is 9. Also, nine times this number is twice the number obtained by reversing the order of digits of the number. Find the number.
Let the one’s digit be ‘a’ and ten’s digit be ‘b’.
therefore no is = 10b + a
Reversed no = 10a + b
Given,
Sum of the digits of a two – digit number is 9.Also, nine times this number is twice the number obtained by reversing the order of the digits.
⇒ a + b = 9 —– (1)
And 9 (10b + a) = 2 (10a + b)
⇒ 90b + 9a = 20a + 2b
⇒ 88b = 11a
⇒ a = 8b
Substituting value of a in eq 1
⇒ 8b + b = 9
⇒ 9b = 9
⇒ b = 1
Thus,
a = 8 (1) = 9
Hence, no is 10(1) + 8 = 18
Q 35 – The area of a triangle gets reduced by 80 sq. units if its length is reduced by 5 units and the breadth is increased by 2 units. If we increase the length by 10 units and decrease the breadth by 5 units, the area is increased by 50 sq. units. Find the length and breadth of the rectangle.
Length and Breadth of rectangle be l and b.
Area of rectangle = lb
(l – 5) (b + 2) = lb – 80
i.e., 2l – 5b + 70 = 0______ ( 1 )
(l + 10) (b – 5) – lb = 50
5l + 10b = 100
Divide both side by 5
l + 2b = 20
l – 2b +20 = 0________ ( 2 )
Multiplying ( 2 ) by 2 , we get
2l – 4b = -40______ ( 3 )
Subtracting ( 3 ) from ( 1 ), we get
-b = -30
b = 30
2l -5(30) = -70
2l = -70 + 150
l = 40
Length = 40 units and Breadth = 30 units .
Q 36 – A train covered a certain distance at a uniform speed. If the train would have been 6 km/hr. faster, it would have taken 4 hours less than the scheduled time and if the train were slower by 6km/ hr., it would have taken 6 hours more than the scheduled time. Find the distance of the journey
Let the actual speed of the train be x km/hr and the actual time taken be y hours. Then,
Distance covered =(xy)km ..(i) [∴ Distance = Speed × Time]
If the speed is increased by 6 km/hr, then time of journey is reduced by 4 hours i.e., when speed is (x+6)km/hr, time of journey is (y−4) hours.
∴ Distance covered = (x + 6) (y − 4)
⇒ xy = (x + 6) (y − 4) [Using (i)]
⇒ − 4x + 6y – 24 = 0
⇒−2x + 3y − 12 = 0 ..(ii)
When the speed is reduced by 6 km/hr, then the time of journey is increased by 6 hours i.e., when speed is (x−6) km/hr, time of journey is (y−6) hours.
∴ Distance covered = (x − 6) ( y + 6)
⇒ xy = (x − 6) ( y + 6 ) [Using (i)]
⇒ 6x − 6y – 36 = 0
⇒x –y – 6 = 0 (iii)
Thus, we obtain the following system of equations:
−2 x + 3y −12 = 0
x – y – 6 = 0
By using cross-multiplication, we have,
⇒ x =30 and y = 24
Putting the values of x and y in equation (i), we obtain
Distance =(30 × 24) km =720 km.
Hence, the length of the journey is 720 km.
Q 37 – For which value (s) of k will the pair of equations kx + 3y = k – 3, 12x + ky = k has no solution ?
kx + 3y = k – 3 …(i)
12x + ky = k …(ii)
On comparing the equations (i) and (ii) with ax + by = c = 0,
We get,
a1 = k, b1 = 3, c1 = – (k – 3)
a2 = 12, b2 = k, c2 = – k
Then,
For no solution of the pair of linear equations,
Taking first two parts, we get
k2 = 36
k = + 6 or – 6
Taking last two parts, we get
3k ≠ k(k – 3)
k2 – 6k ≠ 0
so, k ≠ 0,6
Therefore, value of k for which the given pair of linear equations has no solution is k = – 6.
Q 38 – Write a pair of linear equations which has the unique solution x = -1 and y =3. How many such pairs can you write?
Take the equations as follows:
a1x +b1 y + c1 = 0
a2x +b2 y + c2 = 0
As x = -1,y = 3 is a solution of each of the
equations,
–a1 +3b2 + c1 = 0
– a2 +3b2 + c2 = 0
For different values of a1,b1,c1,a2,b2,c2, we get different equations.
So, there exist many such pairs of equations which has a unique solution
x = – 1 y = 3
Take a1 = 1 b1 =1 c1 = 2 a2 = 2 b2 = 3, c2 = 1
x + y + 2 = 0
2x + 3y + 1 = 0
Hence, there exist infinitely many pairs of equations which has a unique solution x = – 1 y = 3 Also, unique pair of equations is
x + y + 2 = 0, 2x + 3y + 1 = 0