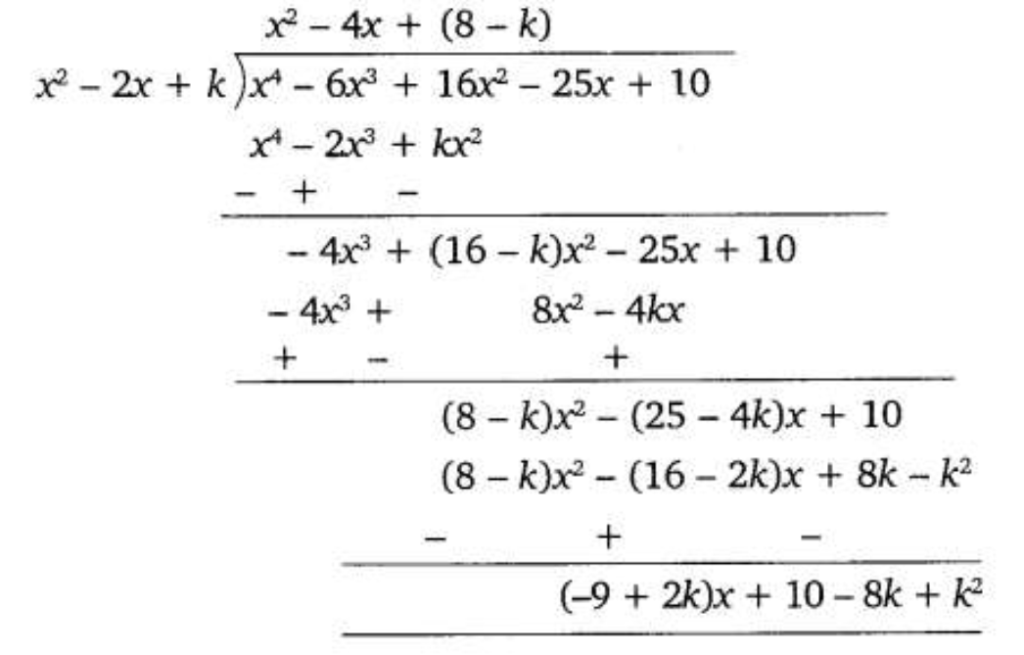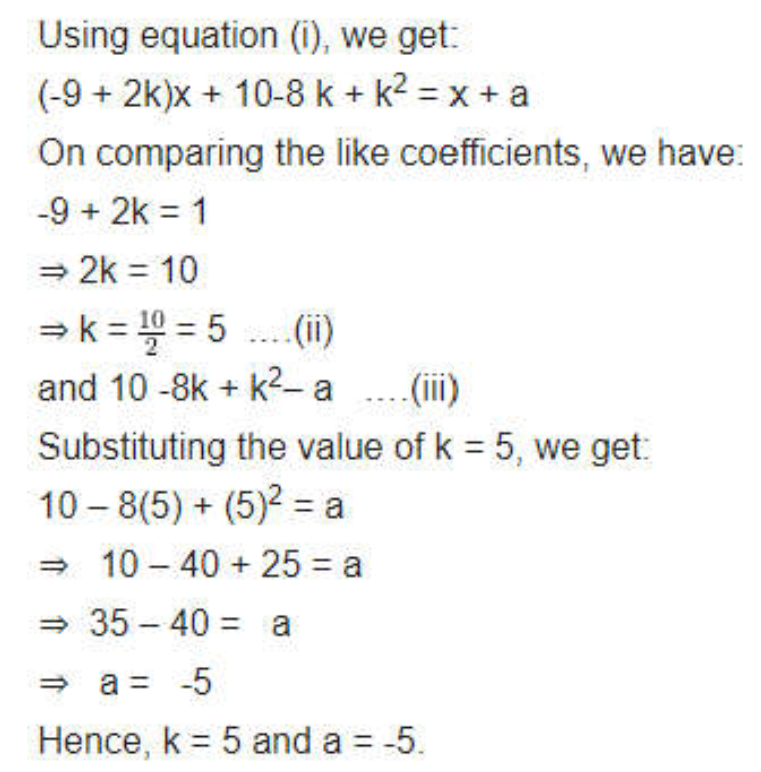Question 1. Verify that the numbers given alongside the cubic polynomials below are their zeroes. Also, verify the relationship between the zeroes and the coefficients in each case:
(i) 2x3 + x2 – 5x + 2; 1/2, 1, -2
(ii) x3 – 4x2 + 5x – 2; 2, 1, 1
Solution:
(i) Comparing the given polynomial with ax3 + bx2 + cx + d, we get
a = 2, b = -1, c = -5 and d = 2
p(x) = 2x3 + x2 – 5x + 2

CLASS-10 MATHS-POLYNOMIALS CHAPTER EX-2.4 OPTIONALS….
(ii) x3 -4x2 +5x -2 ; 2, 1, 1
Solution:
Given, p(x) = x3 – 4x2 + 5x – 2
And zeroes for p(x) are 2,1,1.
∴ p(2)= 23 -4(2)2 +5(2)-2 = 0
p(1) = 13 -(4×12)+(5×1)-2 = 0
Hence proved, 2, 1, 1 are the zeroes of x3 – 4x2 +5x – 2
Now, comparing the given polynomial with general expression, we get;
∴ ax3 +bx2 +cx+d = x3 – 4x2 +5x – 2
a = 1, b = -4, c = 5 and d = -2
As we know, if α, β, γ are the zeroes of the cubic polynomial ax2 +bx2 +cx+d , then;
α + β + γ = –b/a
αβ + βγ + γα = c/a
α β γ = – d/a.
Therefore, putting the values of zeroes of the polynomial,
α +β+γ = 2+1+1 = 4 = -(-4)/1 = –b/a
αβ+βγ+γα = 2×1+1×1+1×2 = 5 = 5/1= c/a
αβγ = 2×1×1 = 2 = -(-2)/1 = -d/a
Hence, the relationship between the zeroes and the coefficients is satisfied.
Question 2.
Find a cubic polynomial with the sum, some of the product of its zeroes taken two at a time, and the product of its zeroes as 2, -7, -14 respectively.
Solution:
Let us consider the cubic polynomial is ax3 +bx2 +cx+d and the values of the zeroes of the polynomials be α, β, γ.
As per the given question,
α+β+γ = -b/a = 2/1
αβ +βγ+γα = c/a = -7/1
α βγ = -d/a = -14/1
Thus, from the above three expressions, we get the values of the coefficient of the polynomial.
a = 1, b = -2, c = -7, d = 14
Hence, the cubic polynomial is x3 – 2x2 -7x+14
Question 3.
If the zeroes of the polynomial x3 – 3x2 + x + 1 are a-b, a, a + b, find a and b.
Solution:
We are given with the polynomial here,
p(x) = x3 -3x2 +x+1
And zeroes are given as a – b, a, a + b
Now, comparing the given polynomial with general expression, we get;
∴px3 +qx2 +rx+s = x3 -3x2 +x+1
p = 1, q = -3, r = 1 and s = 1
Sum of zeroes = a – b + a + a + b
-q/p = 3a
Putting the values q and p.
-(-3)/1 = 3a
a=1
Thus, the zeroes are 1-b, 1, 1+b.
Now, product of zeroes = 1(1-b)(1+b)
-s/p = 1-b2
-1/1 = 1-b2
b2 = 1+1 = 2
b = √2
Hence,1-√2, 1 ,1+√2 are the zeroes of x3 -3x2 +x+1.
CLASS-10 MATHS-POLYNOMIALS CHAPTER EX-2.4 OPTIONALS….
Question 4. If two zeroes of the polynomial x4 – 6x3 – 26x2 + 138x – 35 are 2 ± √3, find other zeroes.
Solution:

Question 5.
If the polynomial x4 – 6x3 + 16x2 – 25x + 10 is divided by another polynomial x2 – 2x + k, the remainder comes out to be x + a, find k and a.
Solution:
We have
p(x) = x4 – 6x3 + 16x2 – 25x + 10
Remainder = x + a…..(i)
Now, we divide the given polynomial 6x3 + 16x2 – 25x + 10 by x2 – 2x + k.