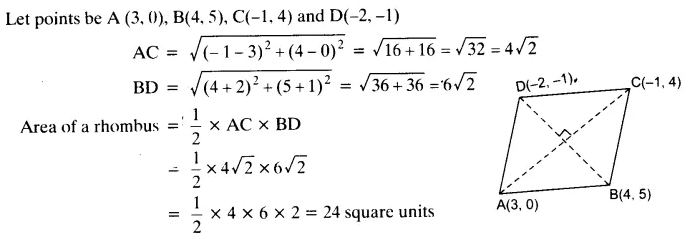NCERT SOLUTIONS FOR CLASS 10 MATHS COORDINATE GEOMETRY CHAPTER 7 EX 7.2
Question 1.
Find the coordinates of the point which divides the join of (-1, 7) and (4, -3) in the ratio 2 : 3.
Solution:
Ex 7.2 Class 10 Maths Question 2.
Find the coordinates of the points of trisection of the line segment joining (4, -1) and (-2, -3).
Solution: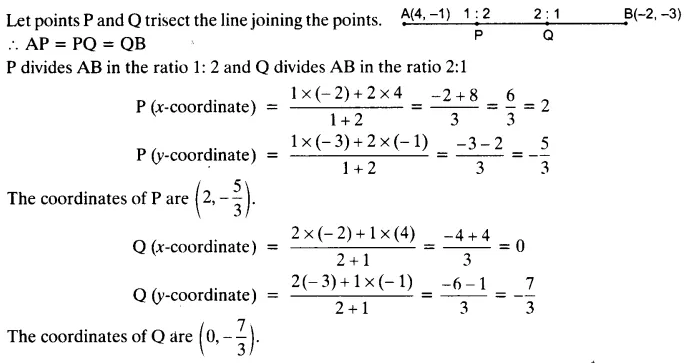
Ex 7.2 Class 10 Maths Question 3.
To conduct Sports Day activities, in your rectangular shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1 m each. 100 flower pots have been placed at a distance of 1 m from each other along AD, as shown in given
figure below. Niharika runs 14 th the distance AD on the 2nd line and posts a green flag. Preet runs 15 th distance AD on the eighth line and posts a red flag. What is the distance between both the flags? If Rashmi has to post a blue flag exactly halfway between the line segment joining the two flags, where should she post her flag?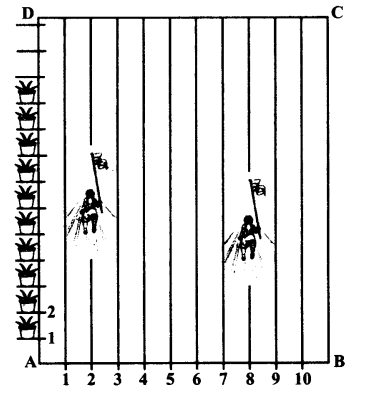
Solution:
The blue flag is in the 5th line, at a distance of 22.5 m.
Ex 7.2 Class 10 Maths Question 4.
Find the ratio in which the line segment joining the points (-3, 10) and (6, -8) is divided by (-1, 6).
Solution:
Ex 7.2 Class 10 Maths Question 5.
Find the ratio in which line segment joining A (1, -5) and B (-4, 5) is divided by the x-axis. Also, find the coordinates of the point of division.
Solution:
Ex 7.2 Class 10 Maths Question 6.
If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.
Solution: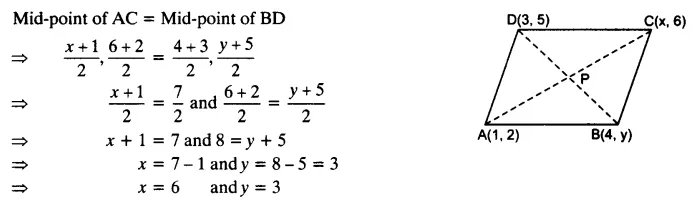
Ex 7.2 Class 10 Maths Question 7.
Find the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, -3) and B is (1, 4).
Solution:
Ex 7.2 Class 10 Maths Question 8.
If A and B are (-2, -2) and (2, -4), respectively, find the coordinates of P such that AP = 37 AB and P lies on the line segment AB.
Solution:
Ex 7.2 Class 10 Maths Question 9.
Find the coordinates of the points which divide the line segment joining A (-2, 2) and B (2, 8) into four equal parts.
Solution:
Ex 7.2 Class 10 Maths Question 10.
Find the area of a rhombus if its vertices are (3, 0), (4, 5), (-1, 4) and (-2, -1) taken in order.
[Hint: Area of a rhombus = 12 (product of its diagonals)]
Solution: