Q 1 – The area of a triangle is’ xy’ where’ x’ is length and ‘y’ is breadth. If the length of a rectangle is increased by 5 units and breadth is decreased by 3 units, the new area of the rectangle will be
(a) (x–y)(x+3)
(b) (xy+15)
(c) (x+5)(y–3)
(d) (xy+5–3)
Q 2 – The volume of a rectangle with length, breadth and height as 5x, 3x2, and 7x4 respectively is:
(a) 105x7
(b) 105x2
(c) 105x4
(d) 105x
Ans. (a) 105x7
Hint:
Volume of rectangle = Length × breadth × height
V = 5x × 3x2 × 7x4
V = 105 x1+2+4
V = 105x7 cubic unit.
Q 3 – The volume of rectangular box whose length, breadth and height is 2p, 4q. 8r respectively is
(a) 14pqr
(b) 2p+4q+8r
(c) 64pqr
(d) 64
Q 4 – If we multiply 5x and (–4xyz), then we get:
(a) 20x2yz
(b) –20x2yz
(c) x2yz
(d) –2xyz
Ans. (b) –20x2yz
Hint:
(5x) x (–4xyz)
= 5 × x × (–4) × x × y × z
= –20x1+1yz
= –20x2yz
Q 5 – The area of a rectangle that has length = 2a²b and breadth = 3ab² is:
(a) 6a³b³
(b) a³b³
(c) 2a³b³
(a) 4a³b³
Ans. (a) 6a³b³
Explanation:
Area of rectangle = (2a²b)(3ab²) = 6a³b³
Q 6 – Factorised Form of p2 – 17p – 38 is
(a) (p – 19) (p + 2)
(b) (p – 19) (p – 2)
(c) (p + 19) (p + 2)
(d) (p + 19) (p – 2)
Ans. (a) (p – 19) (p + 2)
Q 7 – Multiplication of monomials x², (–x)³, (–x)4 is equal to:
(a) x9
(b) x5
(c) x7
(d) x6
Ans. (a) x9
Explanation:
(x²).(–x³).(–x)4 = x9
Q 8 – The value of (x + y) (x + y) + (y – z) (y + z) + (z – x) (z + x) is equal to
(a) 3x²
(b) 3y²
(c) 3z²
(d) 0
Ans. (d) 0
Q 9 – Value of expression ‘a(a2+a +1)+5’ for ‘ a’ = 0 is
(a) a+5
(b) 1
(c) 6
(d) 5
Ans. (d) 5
Q 10 – If x2 +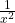 
= 18, find the values of x + 
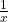and x –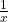
Ans. We know that x2 + 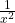= 18
When adding 2 on both sides, we get
x2 + 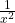+ 2 = 18 + 2
x2 + 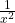+ 2 × x × 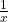= 20
(x + 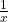)2 = 20
x + 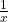= √20
When subtracting 2 from both sides, we get
x2 + 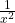– 2 × x × 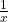= 18 – 2
(x – 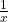)2 = 16
x – 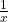= √16
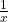x – = 4
Q 11 – Take away:
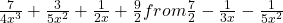
Ans.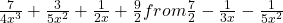
Let us subtract the given expression
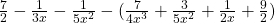
Upon rearranging
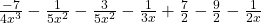
By grouping similar expressions we get,
LCM for (3 and 2 is 6)
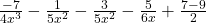
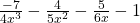
Q 12 – Using the formula for squaring a binomial, evaluate the following:
(999)2
Ans. We can express 999 as 1000 – 1
So, (999)2 = (1000 – 1)2
Upon simplification we get,
(1000 – 1)2 = (1000)2 – 2 (1000) (1) + 12
= 1000000 – 2000 + 1
= 998001
Q 13 – Multiply:
(x – y) and (3x + 5y)
Ans. (x – y) × (3x + 5y) = x × (3x + 5y) – y × (3x + 5y)
= (x × 3x) + (x × 5y) – (y × 3x) – ( y × 5y)
= 3x2 + 5xy – 3yx – 5y2 = 3x2 + 2xy – 5y2 (Adding like terms)
Q 14 – Simplify:
4ab (a–b) – 6a2 (b-b2) –3b2 (2a2 –a) + 2ab (b–a)
Ans.
4ab (a–b) – 6a2 (b–b2) –3b2 (2a2 –a) + 2ab (b–a)
Let us simplify the given expression
4a2b – 4ab2 – 6a2b + 6a2b2 – 6a2b2 + 3ab2 + 2ab2 – 2a2b
By grouping similar expressions we get,
4a2b – 6a2b– 2a2b – 4ab2 + 3ab2 + 2ab2 + 6a2b2 – 6a2b2
–4a2b + ab2
Q 15 – Simplify the expressions and evaluate them as directed:
(i) x (x – 3) + 2 for x = 1,
(ii) 3y (2y – 7) – 3 (y – 4) – 63 for y = –2
Ans.
(i) x (x – 3) + 2 = x2 – 3x + 2
For x = 1, x2 – 3x + 2 = (1)2 – 3 (1) + 2
= 1 – 3 + 2 = 3 – 3 = 0
(ii) 3y (2y – 7) – 3 (y – 4) – 63 = 6y2 – 21y – 3y + 12 – 63
= 6y2 – 24y – 51
For y = –2, 6y2 – 24y – 51 = 6 (–2)2 – 24(–2) – 51
= 6 × 4 + 24 × 2 – 51
= 24 + 48 – 51 = 72 – 51 = 21
Q 16 – Simplify (a + b) (2a – 3b + c) – (2a – 3b) c.
Ans. We have
(a + b) (2a – 3b + c) = a (2a – 3b + c) + b (2a – 3b + c)
= 2a2 – 3ab + ac + 2ab – 3b2 + bc
= 2a2 – ab – 3b2 + bc + ac (Note, –3ab and 2ab are like terms)
and (2a – 3b) c = 2ac – 3bc
Therefore,
(a + b) (2a – 3b + c) – (2a – 3b) c = 2a2 – ab – 3b2 + bc + ac – (2ac – 3bc)
= 2a2 – ab – 3b2 + bc + ac – 2ac + 3bc
= 2a2 – ab – 3b2 + (bc + 3bc) + (ac – 2ac)
= 2a2 – 3b2 – ab + 4bc – ac
Q 17 – Subtract the sum of 3l – 4m – 7n2 and 2l + 3m – 4n2 from the sum of 9l + 2m – 3n2 and -3l + m + 4n2….
Ans.
Sum of 3l – 4m – 7n2 and 2l + 5m – 4n2
3l – 4m – 7n2 + 2l + 3m – 4n2
Upon rearranging
3l + 2l – 4m + 3m – 7n2 – 4n2
5l – m – 11n2 ……………………..equation (1)
Sum of 9l + 2m – 3n2 and -3l + m + 4n2
9l + 2m – 3n2 + (–3l + m + 4n2)
Upon rearranging
9l – 3l + 2m + m – 3n2 + 4n2
6l + 3m + n2 ……………………….equation (2)
Let us subtract equation (i) from (ii), we get
6l + 3m + n2 – (5l – m – 11n2)
Upon rearranging
6l – 5l + 3m + m + n2 + 11n2
l + 4m + 12n2
Q 18 – Find the value of (5x6) × (–1.5x2y3) × (–12xy2) when x = 1, y = 0.5
Ans. Let us simplify the given expression
5 × –1.5 × –12 × x6 × x2 × x × y3 × y2
90 × x6+2+1 × y3+2
90x9y5
Now let us substitute when, x = 1 and y = 0.5
For 90x9y5
90 × (1)9× (0.5)5
2.8125
45/16