Q 1– Solve for x (in terms of a and b)
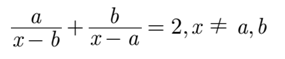
Value of the roots of the quadratic equation, x2 – x – 6 = 0 are ………………..
Ans.
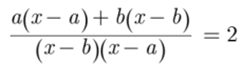
We have

Value of the roots of the quadratic equation, x2– x –6 = 0 are ………….. .

Q 2 – Two concentric circles are of radii 5cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Ans. Let O be the center of the concentric circle of radii 5 cm and 3 cm respectively. Let AB be a chord of the larger circle touching the smaller circle at P.
Then
AP=PB and OP⊥AB
Applying Pythagoras theorem in △OPA, we have
OA2=OP2+AP2
⇒25=9+AP2
⇒AP2=16⇒AP=4 cm
∴AB=2AP=8 cm

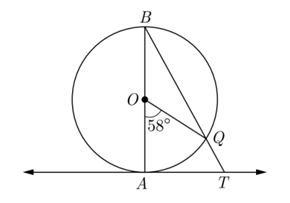
Q 3– In the given figure, AB is the diameter of a circle with center O, and AT is a tangent.
If ∠ AOQ = 58 , find ∠ ATQ.
Ans.
We have ∠AOQ = 58c
Since angle ∠ ABQ and ∠AOQ are the angle on the circumference of the circle by the same arc,

Here OA is perpendicular to TA because OA is radius and TA is tangent at A.
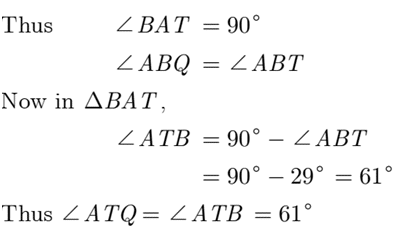
Q 4– A solid is in the form of a cone mounted on a hemisphere with both their radii being equal to 1 cm and the height of the cone being equal to its radius. Find the volume of the solid in terms of π.
Q 5– Find the mean of the following data :
| Class | Frequency |
| 0.5-5.5 | 13 |
| 5.5-10.5 | 16 |
| 10.5-15.5 | 22 |
| 15.5-20.5 | 18 |
| 20.5-25.5 | 11 |
Ans. We prepare the following table to find mean.
| Class | xi = classmark | fi | fi xi |
| 0.5-5.5 | 3 | 13 | 39 |
| 5.5-10.5 | 8 | 16 | 128 |
| 10.5-15.5 | 13 | 22 | 286 |
| 15.5-20.5 | 18 | 18 | 324 |
| 20.5-25.5 | 23 | 11 | 253 |
| Total | ∑fi =80 | 1,030 |
Mean

Q 6– Find the mean number of plants per house from the following data :
| Number of plants | 0-2 | 2-4 | 4-6 | 6-8 | 8-10 | 10-12 | 12-14 |
| Number of houses | 1 | 2 | 1 | 5 | 6 | 2 | 3 |
Or
Consider the following frequency distribution of the heights of 60 students of a class :
| Height (in cm) | 150-155 | 155-160 | 160-165 | 165-170 | 170-175 | 175-180 |
| Number of students | 15 | 13 | 10 | 8 | 9 | 5 |
What is the upper limit of the median class in the given data?
| Number of plants | 0-2 | 2-4 | 4-6 | 6-8 | 8-10 | 10-12 | 12-14 |
| Number of houses | 1 | 2 | 1 | 5 | 6 | 2 | 3 |
Mean
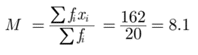
Q 7– Solve the following quadratic equation for x :
9x2 – 9 (a + b) x + 2a2 + 5ab + 2b2 = 0
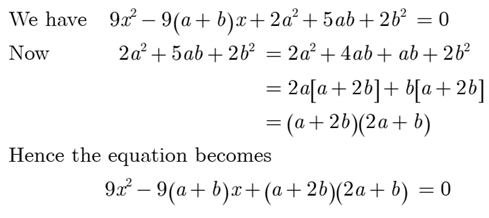
Q 8– The sum of the first n terms of three arithmetic progressions are, S1 S2, and S3 respectively. The first term of each AP is 1 and common differences are 1, 2, and 3 respectively. Prove that S1+S3 =2S2
Ans. Let the first term be a the common difference be d, n th term be an and sum of n term be Sn.
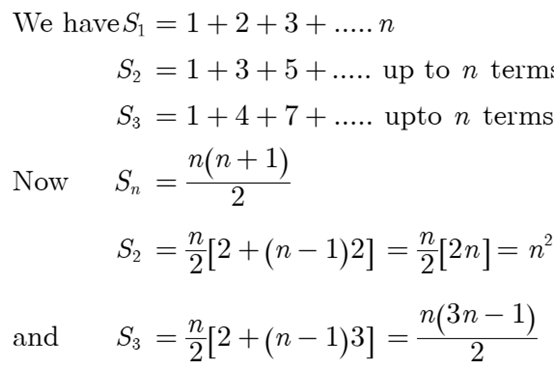

Q 9 – Which term of the AP 3,12, 21, 30 ….. will be 90 more than its 50th term.
Ans.

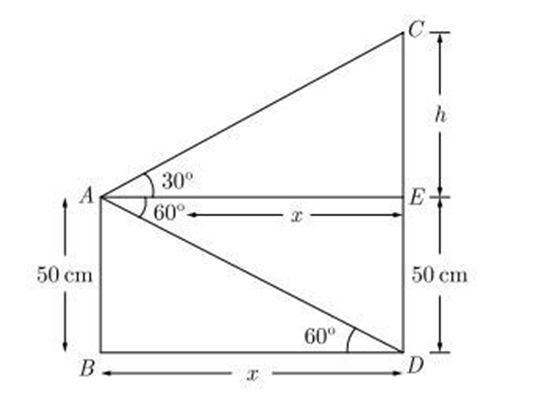
Q 10 – A girl on a ship standing on a wooden platform, which is 50 m above water level, observes the angle of elevation of the top of a hill as 30° and the angle of depression of the base of the hill as 60°. Calculate the distance of the hill from the platform and the height of the hill.
Ans.
The distance between hill and platform is 50√3 / 3 m and height of hill is 66.66m.
Step-by-step explanation:
Let AB be the wooden platform of height 50m. As per question we have shown the figure below. Here total height of hill is CD and h is the height of hill above platform.
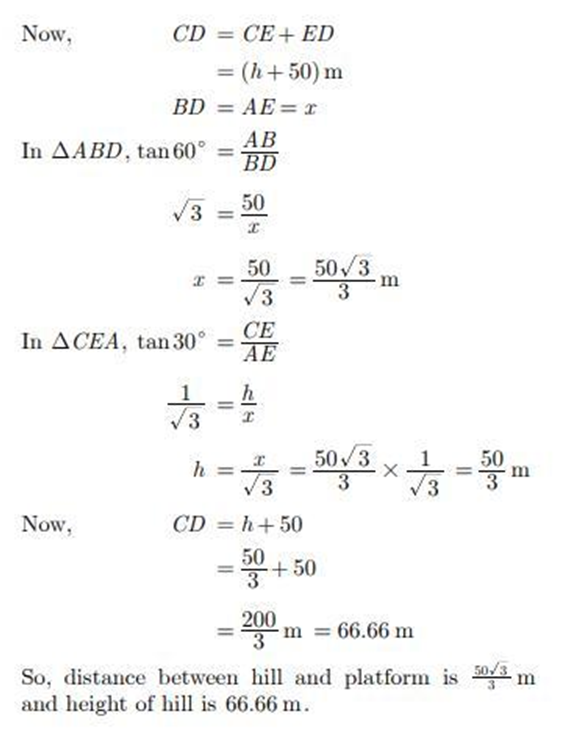
Q 11 – From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45°, respectively. If the bridge is at a height of 30 m from sea level, then find the width of the river.
Ans.

Let the width of river =AB
And the bridge is at a height of 3m from banks
So, DP=3m
Angel of depression of banks on the opposite sides of the river are =300,450
So,∠QPA=300
∠RPB=450
We need to find AB=?
Since PD height so it will be perpendicular at AB
∠PDA=∠PDB=900
And line QR is parallel to line AB
∠PAD=∠QPA=300 (Alternate angle)
Similarly,
∠QPB=∠PBD=450 (Alternate angle)
Now, in triangle PAD
tan30=![]()
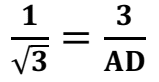
AD=3√3
Now in triangle PBD ,

Q 12 – The window of a house is ‘h’ m above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be α and β respectively. Prove that the height of the other house is h (1+ tanα cotβ)m.
Ans.

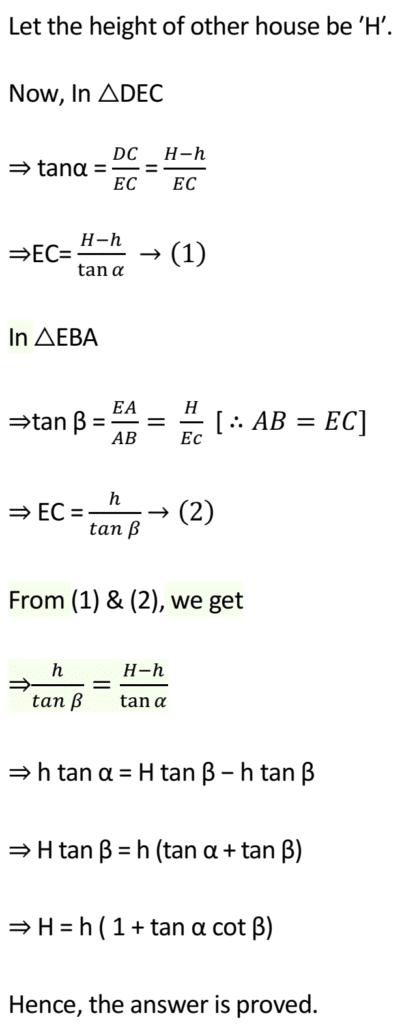
Q 13 – In Figure the radius of in circle of ∆ ABC of area 84 cm2 and the lengths of the segments AP and BP into which side AB is divided by the point of contact are 6 cm and 8 cm Find the lengths of the sides AC and BC.

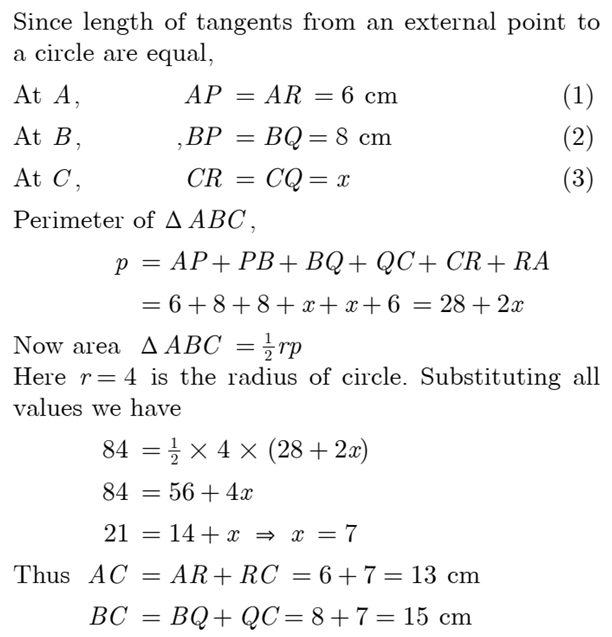
Q 14 – Prove that tangent drawn at any point of a circle perpendicular to the radius through the point contact.
OR
Prove that tangent drawn at any point of a circle perpendicular to the radius through the point contact.
Ans. Consider a circle with center O with tangent AB at point of contact P as shown in the figure below

Let Q be a point on AB and we join OQ. Suppose it touch the circle at R.
We Op = OR (Radius)
OQ > OR
OQ > OP
The same will be the case with all other points on the circle. Hence OP is the smallest line that connects AB and the smallest line is perpendicular.
