CBSE PRACTICE PAPER MATHS FOR CLASS 10 POLYNOMIALS CHAPTER 2
Q 1 – If the roots of the quadratic polynomial are equal, where the discriminant D = b2 – 4ac, then (1 Marks)
a) D > 0
b) D < 0
c) D ≥ 0
d) D = 0
Q 2 – If the sum of the roots is –p and product of the roots is –1/p, then the quadratic polynomial is (1 Marks)
a) k(–px2 + x/p + 1)
b) k(px2 – x/p – 1)
c) k(x2 + px – 1/p)
d) k(x2 – px + 1/p)
Q 3 – If the zeroes of the quadratic polynomial x2 + (a + 1) x + b are 2 and -3, then (1 Marks)
(a) a = -7, b = -1
(b) a = 5, b = -1
(c) a = 2, b = -6
(d) a – 0, b = -6
Q 4 – If a and b are the zeroes of the polynomial x2-11x +30, Find the value of a3 + b3 (1 Marks)
a.134
b.412
c.256
d.341
Q 5 – If the polynomial f(x) = x4 -6x3 + 16x2 – 25x + 10 is divided by another polynomial x2 -2x + k, the remainder comes out to be x + a, find k and a. (1 Marks)
Q 6 – Find all the zeroes of the polynomial x4 – 3x3 + 6x – 4, if two of its zeroes are √2 and -√2 (1 Marks)
Q 7 – If α and β are the zeroes of the polynomial ax2 + bx + c, find the value of α2 + β2 . (1 Marks)
Q 8 – If α and β are the zeroes of a polynomial such that α + β = -6 and αβ = 5, then find the polynomial. (1 Marks)
Q 9 – If on division of a polynomial p(x) by a polynomial g(x), the quotient is zero, what is the relation between the degrees of p(x) and g(x)? (1 Marks)
Q 10 – Find the zeroes of the quadratic polynomial 9t2 – 6t + 1 and verify the relationship between the zeroes and the coefficients. (1 Marks)
Q 11 – Form a quadratic polynomial whose zeroes are (1 Marks)
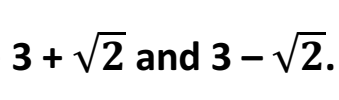
Q 12 – If one of the zeros of the quadratic polynomial (k – 1)x2 + kx + 1 is -3, then find the value of k. (1 Marks)
Q 13 – Find the zeros of the polynomial p(x) = 4x – 12x + 9. (1 Marks)
Q 14 – If the polynomial 6x4 + 8x3 + 17x2 + 21x + 7 is divided by another polynomial 3x2 + 4x + 1, the remainder comes out to be (ax + b), find a and b. (2 Marks)
Q 15 – If -1 and 2 are two zeroes of the polynomial 2x3 – x2 – 5x – 2, find its third zero. (2 Marks)
Q 16 – If 2 and -3 are the zeroes of the quadratic polynomial x2 + (a + 1) x + b; then find the values of a and b. (2 Marks)
Q 17 – If one zero of the polynomial 2x2 + 3x + λ is 1/2 find the value of and other zero. (2 Marks)
Q 18 – Find the zeros of the polynomial f(x) = x3 – 5x2 – 2x + 24, if it is given that the product of its two zeros is 12.(2 marks)
Q 19 – If one zero of polynomial (a2 + 9)x2 + 13x + 6a is reciprocal of the other, find the value of a. (2 Marks)
Q 20 – Divide 2x4 – 9x3 + 5x2 + 3x – 8 by x2 – 4x+ 1 and verify the division algorithm. (2 Marks)
Q 21 – On dividing the polynomial 4x4 – 5x3 – 39x2 – 46x – 2 by the polynomial g(x), the quotient and remainder were x2 – 3x – 5 and -5x + 8 respectively. Find g(x). (2 Marks)
Q 22 – What must be subtracted or added to p(x) = 8 x4 + 14x3 – 2x2 + 8x – 12 so that 4x2 + 3x – 2 is a factor of p(x)? (3 Marks)
Q 23 – On dividing 3x3 + 4x2 + 5x – 13 by a polynomial g(x) the quotient and remainder were 3x +10 and 16x – 43 respectively. Find the polynomial g(x). (3 Marks)
Q 24 – What must be subtracted from p(x) = 8x4 + 14x3 – 2x2 + 7x – 8 so that the resulting polynomial is exactly divisible by g(x) = 4x2 + 3x – 2? (3 Marks)
Q 25 – If the polynomial f(x) = x4 – 6x3 + 16x2 – 25x + 10 is divided by another polynomial x2 – 2x + k, the remainder comes out to be x + a. Find k and a. 3 Marks)
Q 26 – Find the zeros of the polynomial f(x) = – 12x2 + 39x – 28, if it is given that the zeros are in AP. (3 Marks)
Q 27 – If and β are the zeros of the quadratic polynomial f (x) = ax2 + bx + c, then evaluate: (3 Marks)
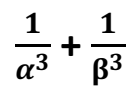
Q 28 – If the zeros of the polynomial f(x) = ax3 + 3bx2 + 3cx + d are in A.P., prove that 2b3 – 3abc + a2d = 0. (3 Marks)
Q 29 – If two zeros of the polynomial f(x) = x4 – 6x3 – 26x2 + 138x – 35 are 2 ,find other zeros. (3 Marks)
Q 30 – Given that x- is a factor of the cubic polynomial x3 – 3 x2 + 13x – 3, find all the zeroes of the polynomial. (3 Marks)