CBSE Maths Formula Class 10 Introduction to Trigonometry Chapter 8
Class-10 Introduction to Trigonometry Students will study some ratios of the sides of a right triangle with respect to its acute angles called trigonometric ratios of the angle. We will restrict our discussion to acute angles only. However, these ratios can be extended to other angles also. We will also define the trigonometric ratios for angles of measure 0° and 90°. We will calculate trigonometric ratios for some specific angles and establish some identities involving these ratios, called trigonometric identities.
Class-10 Introduction to Trigonometry The values of the trigonometric ratios of an angle do not vary with the lengths of the sides of the triangle if the angle remains the same.
You can more questions for Class 10 click www.cbseinsights.com


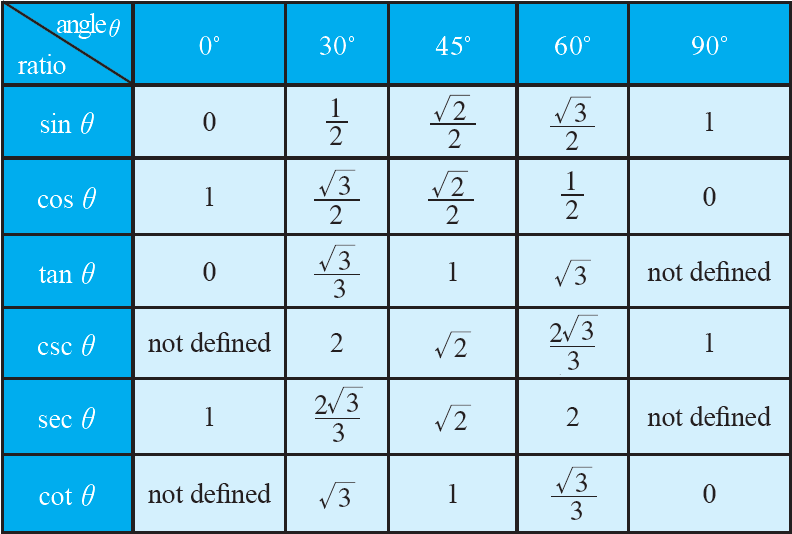
Trigonometric Ratios of Common angles:
We can find the values of trigonometric ratio’s various angle.
Summary
Class-10 Introduction to Trigonometry
Students will studied the following points :
1. In a right triangle ABC, right-angled at B,
sin A = side opposite to angle A / hypotenuse,
cos A = side adjacent to angle A / hypotenuse
tan A = side opposite to angle A / side adjacent to angle A .
2. Cosec A = 1 / Sin A ,
sec A = 1 / Cos A
tan A = 1 / Cot A
tan A = sin A / cos A
3. If one of the trigonometric ratios of an acute angle is known, the remaining trigonometric ratios of the angle can be easily determined.
4. The values of trigonometric ratios for angles 0°, 30°, 45°, 60° and 90°.
5. The value of sin A or cos A never exceeds 1, whereas the value of sec A or cosec A is always greater than or equal to 1.
6. sin (90° – A) = cos A, cos (90° – A) = sin A;
tan (90° – A) = cot A, cot (90° – A) = tan A;
sec (90° – A) = cosec A, cosec (90° – A) = sec A.
7. sin2 A + cos2 A = 1,
sec2 A – tan2 A = 1 for 0° ≤ A < 90°,
cosec2 A = 1 + cot2 A for 0° < A ≤ 90º.