CBSE Maths Formula Class 10 Quadratic Equations Chapter 4
Class-10 Quadratic Equations Students can easily learn and step by step solve the questions. For More questions related to class 10 maths One type was the quadratic polynomial of the form ax2 + bx + c, a ≠ 0. When we equate this polynomial to zero, we get a quadratic equation. Quadratic equations come up when we deal with many real-life situations.
Students can also do all questions for NCERT Maths Books.

How to Solve Quadratic equation:
Class-10 Quadratic Equations


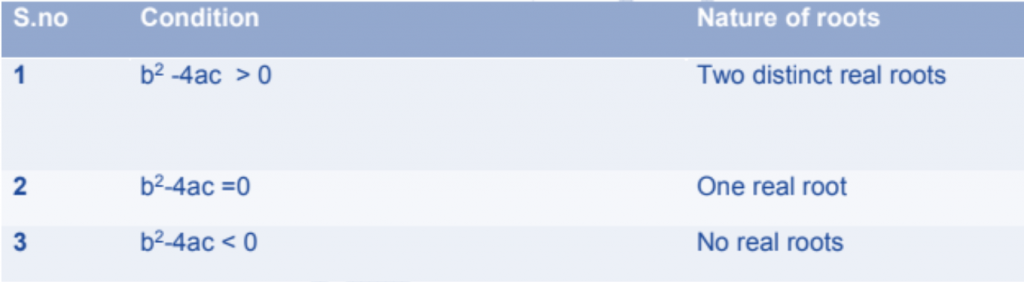
Nature of roots of Quadratic equation:
Class-10 Quadratic Equations
Summary
Class-10 Quadratic Equations
1. A quadratic equation in the variable x is of the form ax2+ bx + c = 0, where a, b, c are real numbers and a ≠ 0.
2. A real number α is said to be a root of the quadratic equation ax2 + bx + c = 0, if aα2 + bα + c = 0. The zeroes of the quadratic polynomial ax2 + bx + c and the roots of the quadratic equation ax2 + bx + c = 0 are the same.
3. If we can factorise ax2 + bx + c, a ≠ 0, into a product of two linear factors, then the roots of the quadratic equation ax2 + bx + c = 0 can be found by equating each factor to zero.
4. A quadratic equation can also be solved by the method of completing the square.
5. Quadratic formula: The roots of a quadratic equation ax2 + bx + c = 0 are given by
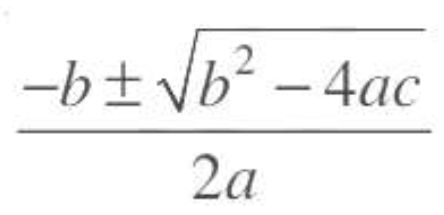
provided b2 – 4ac ≥ 0.
6. A quadratic equation ax2 + bx + c = 0 has
(i) two distinct real roots, if b2 – 4ac > 0,
(ii) two equal roots (i.e., coincident roots), if b2 – 4ac = 0, and
(iii) no real roots, if b2 – 4ac < 0.