Linear Equations in One Variable Maths important Questions for the concept clarity of the Students. We, at cbseinsights.com have prepared these questions with detailed explanations for the betterment of the students.
Q 1 – The standard form of a linear equation in one variable x is (1 Marks)
(a) ax + b = 0
(b) ax² + bx + c = 0
(c) ax³ + bx² + cx + d = 0
(d) ax + bx³ + cx² + dx + e = 0
Ans. (a) ax + b = 0
Q 2 – The difference between two whole numbers is 66. The ratio of the two numbers is 2 : 5. The two numbers are: (1 Marks)
a) 60 and 6
b) 100 and 33
c) 110 and 44
d) 99 and 33
Ans. c) 110 and 44
Let the no’s be 2x & 5x .
As per the question,
5x – 2x = 66
3x = 66
x = 22 .
Therefore, the no’s are 110 and 44
Q 3 – The statement ‘on adding 10 in a number, the number becomes 20’ in the form of an equation is (1 Marks)
(a) x – 10 = 20
(b) x + 10 = 20
(c) 10x = 20
(d) x/ 2= 20
Ans. (b) x + 10 = 20
Q 4 – What should be added to –7/3 to get 3/7? (1 Marks)
a) 21/58
b) 58/21
c) 47/2
d) 50/21
Ans. (b) 58/21
Explanation: Let the number be x
–7/3 + x = 3/7
x = 3/7 + 7/3 = (9 + 49) / 21 = 58 / 21
Linear Equations in One Variable Questions……
Q 5 – Seven times a number is 42. This statement in the form of an equation is (1 Marks)
(a) x + 7 = 42
(b) 7x = 42
(c) x = 42
(d) x – 7 = 42
Ans. (b) 7x = 42
Q 6 – If 6 is added to 3 times of a number, it becomes 15. This statement in the form of an equation is (1 Marks)
(a) 3x + 6 = 15
(b) 3x – 6 = 15
(c) 3x + 15 = 6
(d) 3x/6= 15
Ans. (a) 3x + 6 = 15
Q 7 – If x is an even number then the consecutive even number is (1 Marks)
(a) x + 1
(b) x + 2
(c) 2x
(d) x – 1
Ans. (b) x + 2
Q 8 – The root of the equation 14 – x = 8 is (1 Marks)
(a) 2
(b) 4
(c) 6
(d) 8
Ans. (c) 6
The root of any algebraic expression or equation is that value of x , for which the value of polynomial becomes Zero.
Therefore, Solving for the value of x
14 – x = 8 is (1 Marks)
– x = 8 – 14 .
– x = – 6
x = 6
Q 9 – The solution of 2x – 3=7 is: (1 Marks)
a) 5
b) 7
c) 12
d) 11
Ans. a)
Explanation:
2x – 3 = 7
2x = 7 + 3 = 10
x = 10/2 = 5
Q 10 – Solve for : 0.35 x – 0.025 = 0.32 x + 0.023 (2 Marks)
Solution. 0.35 x – 0.025 = 0.32 x + 0.023
Rearranging the Algebraic equation
0.35 x – 0.32 x = 0.025 + 0.023
0.032 x = 0.048
3/100 x = 48/1000
x = 48/10 x 3
x = 16/10
x = 16
Q 11 – The sum of the two consecutive odd numbers is 36. Find the larger number. (2 Marks)
Ans. Let the two consecutive odd integers be 2n–1 and 2n+1.
so their sum, 4n = 36 i.e. n = 9.
so, the two integers are 17 and 19.
Linear Equations in One Variable Questions……
Q 12 – The sum of a two-digit number and the number obtained by reversing its digits is 121. Find the number if its unit place digit is 5. (2 Marks)
Ans. Step-by-step explanation:
65 + 56 = 121
Let the digits of the two-digit no. be t and 5. Note:- Here t is at Tens Place and 5 is at One’s Place .
The number formed out of the digits will be [ t x 10{tens place} + 5 x 1 { one’s place}]
then on reversing the digits of the no. , we will get 5 and t. Note:- Here 5 is at Tens place and t is at One’s place.
Therefore, the number formed out of the digits will be [ 5 x 10{tens place} + t x 1 { one’s place}]
As per the statement of the question,
[t x 10 + 5 + 5 x 10 + t] =121
11t + 55 = 121 .
11t = 66 .
t = 6
So, number = 65
Q 13 – A boy gets 3 marks for each correct sum and loses 1 mark for each incorrect sum. He does 25 sums and obtains 67 marks. Then how many correct sums were there? (2 Marks)
Ans. Let the total number of correct sums = x.
Then the total number of incorrect sums = 24 – x .
Given that he gets 3 marks for each correct answer and loses 2 marks for each incorrect sum. and he obtained 37 marks.
3x – (24 – x ) x 2 = 37
3x – 48 + 2x = 37
5x – 48 = 37
5x = 37 + 48
5x = 85
x = 85/5
x = 17.
Therefore the number of correct sums = 17.
Q 14– Ram and Mohan have Rs 60000 together. If Ram has Rs 8000 more than Mohan, then find how much money Ram has? (2 Marks)
Ans. Step-by-step explanation:
Let Mohan has Rs. x .
Ram has Rs.8000 more than Mohan. Therefore, Ram has Rs. (x + 8000) .
As per the question,
(x + 8000) + x = 60000 .
2x + 8000 = 60000 .
2x = 60000 – 8000 .
2x = 52000 .
x = Rs. 26000 .
Therefore Ram has Rs. 34,000 /-
Linear Equations in One Variable Questions……
Q 15 – If the side of chess board is smaller than its perimeter by 21 cm, then find the side of the chess board. (2 Marks)
Ans. 7 cm
Step-by-step explanation:
Since chess board is of square shape, let the length of a side be a
Then given that a = 4a – 21
So 3a=21
a = 7 cm
Q 16 – Find the value of x in the equation (2 Marks)
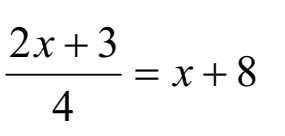
Solution.
2x/4 + 3 / 4 = x + 8
2x/4 – x = 8 – 3/4
2x/4 – 4x / 4 = (32 – 3) / 4
–2x/4 = 29/4
–2x = 29
x = –29/2

Solution. As both the ratios are in proportion, we will cross multiply the ratios .
5 x ( 3 – 2 y ) = 2 x (y + 6 )
15 – 10 y = 2 y + 12
– 12 y = – 3
y = 1/4
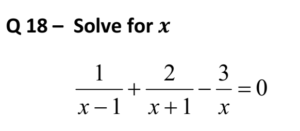
Solution.
Taking LCM of denominators
{(x + 1)x + 2x (x – 1) – 3(x + 1) (x – 1)} / {x (x + 1)(x – 1)} = 0
x2 + x + 2x2 – 2x – 3x 2 + 3 =0
– x + 3 = 0
x = 3
Linear Equations in One Variable Questions……
Q 19 – The angles of a triangle are in the ratio 2 : 3 : 4. Find the angles of the triangle. (3 Marks)
Solution.
The angles of triangle are 40, 60 and 80.
Step-by-step explanation:
It is given that the angle of triangle are in the ratio 2 : 3 : 4. Let the angles are 2x, 3x and 4x.
According to the angle sum property, the sum of interior angles of a triangle is 180 degree.
2x + 3x + 4x = 180
9x = 180
x = 20
The value of x is 20
2 x = 2(20) = 40
3 x = 3(20) = 60
4 x = 4(20) = 80
Therefore the angles of triangle are 40, 60 and 80.
Q 20 – If the sum of two consecutive numbers is 11, find the numbers. (3 Marks)
Solution.
Let the two consecutive integers are x and x + 1 .
According to the question,
x + (x + 1) = 11
2x = 11 – 1
2x = 10
x = 10/2
x = 5.
Therefore ,
Two Integers are 5 and 6.
Q 21 – The difference between two positive numbers is 40 and the ratio of these integers is 1: 3. Find the integers.(3 Marks)
Solution.
Step-by-step explanation:
Let the integers be x and 3x
According to the question
3x – x = 40
2x = 40
x = 40 / 2
x = 20
So, x = 20 and 3x = 20 × 3 = 60