Q 1 – The exterior angle sum of a convex polygon with the number of
sides n is _______. (1 Marks)
A. (n – 2) 180°
B. (n – 2) 90°
C. (n – 2) 270°
D. 360°
Ans. D. 360°
Q 2 – The measures of two adjacent angles of a parallelogram are in the ratio 3:2. Find the measure of each of the angles of the parallelogram? (1 Marks)
A. 110°, 70°
B. 108°, 72°
C. 106°, 74°
Ans. B. 108°, 72°
Q 3 – ABCD is a parallelogram as shown. Find x and y. (1 Marks)
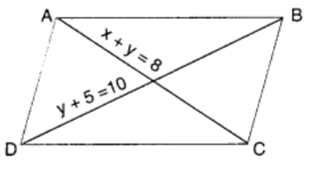
(a) 1, 7
(b) 2, 6
(c) 3, 5
(d) 4, 4
Ans. (c) 3, 5
Hint:
x + y = 8
y + 5 = 10 ⇒ y = 5
∴ x + 5 = 8 ⇒ x = 3.
Q 4 – ABCD is a parallelogram. The angle bisectors of ∠A and ∠D meet at O. What is the measure of ∠AOD? (1 Marks)
(a) 45°
(b) 90°
(c) 75°
(d) 180°
Ans. (b) 90°
Q 5 – The angles of a quadrilateral are in the ratio of 2 : 3 : 5 : 8. Find the measure of each angle. (1 Marks)
Ans. Sum of all interior angles of a quadrilateral = 360°
Let the angles of the quadrilateral be 2x°, 3x°, 5x° and 8x°.
2x + 3x + 5x + 8x = 360°
⇒ 18x = 360°
⇒ x = 20°
Hence the angles are 2 × 20° = 40°,
3 × 20° = 60°,
5 × 20° = 100°
and 8 × 20° = 160°
Q 6 – In a parallelogram ∠A : ∠B = 1 : 2. Then, ∠A = (1 Marks)
(a) 30°
(b) 60°
(c) 45°
(d) 90°
Ans. (b) 60°
Hint:
∠A + ∠B = 180°
∠A : ∠B = 1 : 2
Sum of the ratios = 1 + 2 = 3
∴ ∠A = 1 / 3 × 180° = 60°
Q 7 – P and R are two opposite angles of a parallelogram. If ∠ P = 70°,
then ∠R = ________ (1 Marks)
A. 110°
B. 90°
C. 70°
Ans. C. 70°
Q 8 – Polygons that have any portions of their diagonals in their exteriors are called: (1 Marks)
(a) Squares
(b) Triangles
(c) Convex
(d) Concave
Ans. (c) Convex
Q 9 – If ABCD is an isosceles trapezium, what is the measure of ∠C? (1 Marks)
(a) ∠B
(b) ∠A
(c) ∠D
(d) 90°
Ans. (c) ∠D
Q 10 – Find the perimeter of the rectangle ABCD. (1 Marks)
(a) 6 cm
(b) 12 cm
(c) 3 cm
(d) 24 cm
Ans. (b) 12 cm
Hint:
Perimeter = 2 (4 + 2) cm = 12 cm.
Q 11 – Sum of all interior angles of a polygon with (n) sides is given by: (1 Marks)
(a) (n – 2) × 180°
(b) n – 2 × 180°
(c) (n + 2) × 180°
(d) n + 2 × 180°
Ans. (a) (n – 2) × 180°
Q 12 – The perimeter of a parallelogram is 180 cm. If one side exceeds the other by 10 cm, what are the sides of the parallelogram? (1 Marks)
(a) 40 cm, 50 cm
(b) 45 cm each
(c) 50 cm each
(d) 45 cm, 50 cm
Ans. (a) 40 cm, 50 cm
Q 13 – Two adjacent sides of a rectangle are equal. The name of the quadrilateral is (1 Marks)
(a) square
(b) kite
(c) rhombus
(d) none of these
Ans. (a) square
Q 14 – How many sides does a regular polygon have if the measure of an exterior angle is 24° ? (2 Marks)
Ans. Each exterior angle = Sum of exterior angles/Number of sides
24° = 360°/ Number of sides
⇒ Number of sides = 360° / 24° = 15
Thus, the regular polygon have 15 sides.
Q 15 – The measures of two adjacent angles of a parallelogram are in the ratio 3 : 2. Find the measure of each of the angles of the parallelogram. (2 Marks)
Ans. Let the measures of two adjacent angles ∠A and ∠B be 3x and 2x respectively in parallelogram ABCD.
∠A + ∠B = 180°
⇒ 3x + 2x = 180°
⇒ 5x = 180°
⇒ x = 36°
We know that opposite sides of a parallelogram are equal.
∠A = ∠C = 3x = 3 × 36° = 108°
∠B = ∠D = 2x = 2 × 36° = 72°
Q 16 – In a parallelogram ABCD , If the measure of B exceeds the measure of A by 50˚, find the measure of B. (2 Marks)
Ans.
As Angles ∠ A & ∠ B are adjacent angles of parallelogram
∠ A + ∠ B = 180 ° (Co –interior Angles)
Let ∠ A = x °
As per question
∠ B = 50 ° + x °
Now Put ∠ A & ∠ B in equation 1
∠ x ° + 50 ° + ∠ x ° = 180 °
2 ∠ x + 50 ° = 180 °
2 ∠ x = 130 °
∠ x = 65 °
Q 17 – If all the four sides of a parallelogram are equal and the adjacent angles are of 120° and 60°, then the name of the quadrilateral is (2 Marks)
(a) rectangle
(b) square
(c) rhombus
(d) kite
Ans. (c) rhombus
Q 18 – In the above figure both RISK and CLUE are parallelograms. Find the value of x. (2 Marks)
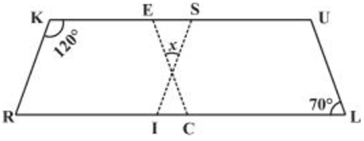
Ans.
∠K + ∠R = 180° (adjacent angles of a parallelogram are supplementary)
⇒ 120° + ∠R = 180°
⇒ ∠R = 180° – 120° = 60°
also, ∠R = ∠SIL (corresponding angles)
⇒ ∠SIL = 60°
also, ∠ECR = ∠L = 70° (corresponding angles)
x + 60° + 70° = 180° (angle sum of a triangle)
⇒ x + 130° = 180°
⇒ x = 180° – 130° = 50°
Q 19 – Find the measure of ∠P and ∠S if SP || RQ ? in Fig 3.34. (If you find m∠R, is there more than one method to find m∠P?) (3 Marks)
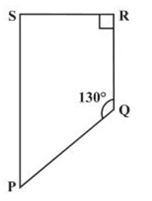
Ans. ∠P + ∠Q = 180° (angles on the same side of transversal)
⇒ ∠P + 130° = 180°
⇒ ∠P = 180° – 130° = 50°
also, ∠R + ∠S = 180° (angles on the same side of transversal)
⇒ 90° + ∠S = 180°
⇒ ∠S = 180° – 90° = 90°
Thus, ∠P = 50° and ∠S = 90°
Yes, there are more than one method to find m∠P.
PQRS is a quadrilateral. Sum of measures of all angles is 360°.
Since, we know the measurement of ∠Q, ∠R and ∠S.
∠Q = 130°, ∠R = 90° and ∠S = 90°
∠P + 130° + 90° + 90° = 360°
⇒ ∠P + 310° = 360°⇒ ∠P = 360° – 310° = 50°
Q 20 – ABC is a right-angled triangle and O is the midpoint of the side opposite to the right angle. Explain why O is equidistant from A, B and C. (The dotted lines are drawn additionally to help you). (3 Marks)
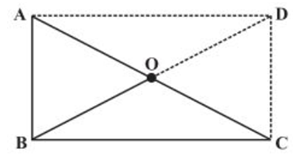
Ans. AD and DC are drawn so that AD || BC and AB || DC
AD = BC and AB = DC
ABCD is a rectangle as opposite sides are equal and parallel to each other and all the interior angles are of 90°.
In a rectangle, diagonals are of equal length and also bisects each other.
Hence, AO = OC = BO = OD
Thus, O is equidistant from A, B and C.