Q 1 – The degree of the equation x² – 2x + 1 = x² – 3 is (1 Marks)
(a) 1
(b) 2
(c) 0
(d) 3
Ans. (a) 1
Hint:
x² – 2x + 1 = x² – 3
⇒ 2x = 4
Q 2 – Which of the following is not a linear equation in one variable? (1 Marks)
(a) 33
(b) 33 (x+ 𝑦)
(c) 33
(d) 33y
Ans. (b) 33 ( x + 𝑦)
Explanation: In 33 (x+y), x and y are two variables.
Q 3 – Which of the following is the Multiplicative identity for rational numbers? (1 Marks)
(a) 1
(b) – 1
(c) 0
(d) None of these
Ans. (a) 1
Q 4 – If 9 is added to a number, it becomes 25. This statement in the form of an equation is (1 Marks)
(a) x+ 9 = 25
(b) x – 9 = 25
(c) 9 x = 25
(d) x / 9 = 25
Ans. (a) x + 9 = 25
Hint:
Let the number be x.
Q 5 – The perimeter of rectangle is 20 cm. If the length of rectangle is 6 cm, then its breadth will be: (1 Marks)
a) 4 cm
b) 6 cm
c) 10 cm
d) 14 cm
Ans. a) 4 cm
Explanation: Perimeter of rectangle = 2 (Length + Breadth)
20 = 2(6 + x)
6 + x = 20/2
6 + x = 10
x = 10 – 6
x = 4 cm
Q 6 – A number when divided by 5 gives 6. This statement in the form of an equation is (1 Marks)
(a) x – 5 = 6
(b) x + 5 = 6
(c) x / 5 = 6
(d) 5 x = 6.
Ans. (c) x / 5 = 6
Hint:
Let the number be x.
Q 7 – Three consecutive integers add up to 51. The integers are: (1 Marks)
a) 16, 17, 18
b) 15, 16, 17
c) 17, 18, 19
d) 18, 19, 20
Ans. a) 16, 17, 18
Explanation: Let the three consecutive integers be x, x+1, x+2
x+(x+1)+(x+2) = 51
3x+3 = 51
3x = 51 – 3
x = 48/3 = 16
x+1 = 16+1=17
x+2 = 16+2 = 18
Q 8 – Which of the following is the reciprocal of a rational number? (1 Marks)
(a) –1
(b) 1
(c) 0
(d) The number itself
Ans. (d) The number itself
Q 9 – The root of the equation 2x + 3 = 2 (x – 4) is (1 Marks)
(a) 2
(b) 4
(c) 0
(d) does not exist
Ans. (d) does not exist
Hint:
2x + 3 = 2 (x – 4)
⇒ 2x + 3 = 2x – 8
⇒ 3 = – 8 which is impossible.
Q 10 – Find the multiplicative inverse of –13. (1 Marks)
(a) 13
(b) – 13
(c) –1 / 13
(d) 12
Ans. (c) –1 / 13
Q 11 – The difference between the two numbers is 21. The larger number is x. The smaller number is (1 Marks)
(a) 21 + x
(b) 21 – x
(c) x – 21
(d) – x – 21
Ans. (c) x – 21
Hint:
x – smaller number = 21
⇒ smaller number = x – 21
Q 12 – Which of the following is the identity element under addition? (1 Marks)
(a) 1
(b) –1
(c) 0
(d) None of these
Ans. (c) 0
Q 13 – Solve : ( x – 2) + ( x – 3) + ( x – 9) = 0 (2 Marks)
Ans. (𝑥 – 2) + (𝑥 – 3) + (𝑥 – 9) = 0
𝑥 – 2 + 𝑥 – 3 + 𝑥 – 9 = 0
3𝑥 – 2 – 3 – 9 = 0
3𝑥 – 14 = 0
𝑥 = 14 / 3
Q 14 – A positive number is 5 times another number. If 21 is added to both the numbers, then one of the new numbers becomes twice of other new numbers. Find the original numbers. (2 Marks)
Ans. Let the smaller number be 𝑥
And another number = 5𝑥
If 21 is added to both the numbers then as per the given condition;
5𝑥 + 21 = 2 × (𝑥 + 21)
5𝑥 + 21 = 2𝑥 + 42
5𝑥 – 2𝑥 = 42 – 21
3𝑥 = 21
𝑥 = 21 / 3= 7
Therefore, the positive number is = 5 × 7 = 35
Q 15 – If x = –1, 𝑦 = 5 and 𝑧 = 10 , verify that x × (𝑦 × z ) = ( x × 𝑦) × 𝑧 (2 Marks)
Ans. Put the given values x = –1, 𝑦 = 5 and 𝑧 = 10 in the
given equation x × (𝑦 × z ) = ( x × 𝑦) × 𝑧
– 1 × (5 × 10) = ( – 1 × 5) × 10
– 50 = – 50
As, L.H.S = R.H.S
... the equation x × (𝑦 × z ) = ( x × 𝑦) × 𝑧 is verified.
Q 16 – Five years ago, Anu was thrice as old as Sonu. After ten years, Anu will be twice as old as Sonu. How old are Anu and Sonu? (2 Marks)
Ans. Let us assume the present ages of Anu is and Sonu is y.
According to the question:
𝑥 – 5 = 3(y – 5)
𝑥 – 5 = 3y – 15
𝑥 = 3y – 15 + 5
𝑥 = 3y -10 ……………….. (1)
Again, as per question;
𝑥 + 10 = 2(y + 10)
𝑥 + 10 = 2y + 20
𝑥 – 2y = 10
(3y – 10) – 2y = 10 (from equation 1)
3y – 2y =10 + 10
y= 20
Substitute, y = 20 in equation 1,
𝑥 = 3 (20) -10
𝑥 =60 – 10
𝑥 = 50
Hence, the present ages of Anu is 50 years and of Sonu is 20 years.
Q 17 – Three consecutive integers are as such they are taken in increasing order and multiplied by 2, 3, and 4, respectively, they add up to 56. Find these numbers. (2 Marks)
Ans. Let us say the three consecutive numbers be x , x +1 and x +2.
Now as per the given question;
2×( x)+3×( x +1)+4×( x+2)=56
9 x + 11 = 56
9 x= 56-11
9 x = 45
x = 45/9
x = 5
Therefore, the three consecutive numbers are 5, 6 and 7.
Q 18 – Find five rational numbers between -3 / 2 and 5 / 3 . (2 Marks)

Q 19 – The denominator of a fraction is greater than the numerator by 8. If the numerator is increased by 17 and the denominator is decreased by 1, the number obtained is 3/2. Find the fraction. (2 Marks)
Ans. Let the numerator of a fraction be x.
Denominator = ( x + 8 )
Fraction = Numerator/Denominator = x / x+8
According to the question,
(x + 17) / (x + 8 – 1) = 3/2
(x + 17) / (x + 7) = 3/2
2 (x + 17 ) = 3 ( x+ 7 )
2x + 34 = 3x + 21
3x – 2x = 34 – 21
x = 13
Numerator = x = 13
And
Denominator = x + 8 = 13 + 8 = 21
Fraction = 13 / 21
Q 20 – The overall width in cm of several wide-screen televisions are 97.28 cm,
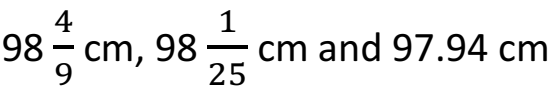
Express these numbers as rational numbers in the form of p and q and arrange the width in ascending orders. (3 Marks)

Q 21 – A bus at a uniform speed covers a distance of
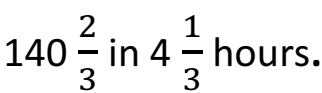
Find the speed of the bus and the distance covered in 6 hours. (3 Marks)



Q 23 – A train travels 1445 / 2 km in 17/2 hours. Find the speed of the train in km/h. (3 Marks)
