Laws of Reflection
The incident ray, reflected ray and the normal all lie in the same plane. Angle of incidence = Angle of reflection
[∠i=∠r]

Propagation of light
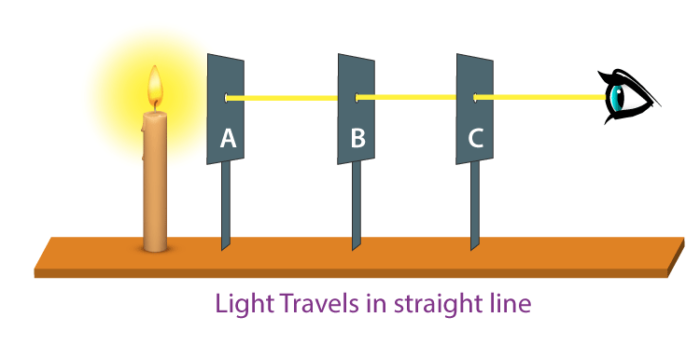
Rectilinear propagation of light: Light travels in a straight line between any two points.
Fermat’s Theorem
The principle of least time: Light always takes the quickest path between any two points (which may not be the shortest path).
Rectilinear propagation of light and the law of re§ection [∠i=∠r] can be validated by Fermat’s principle of least time.
Image formation by a plane mirror
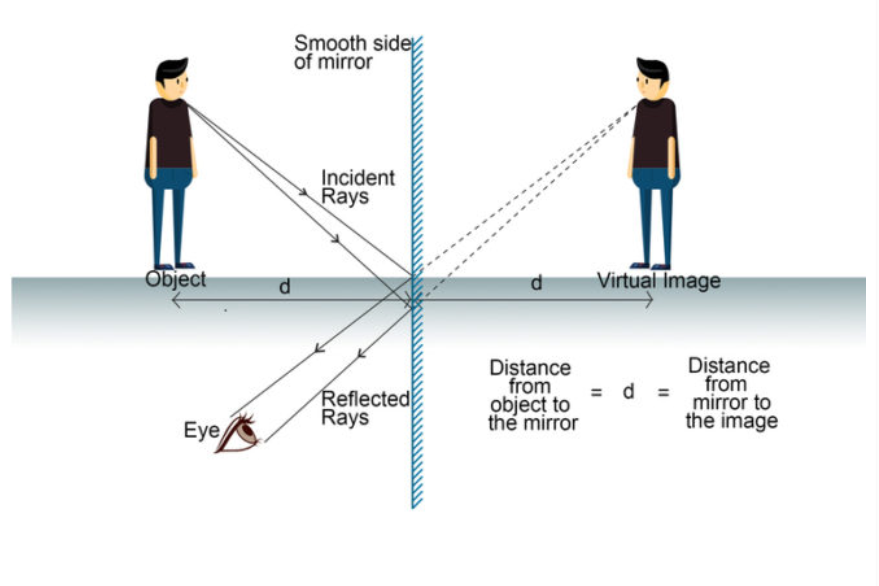
The image formed by a plane mirror is always virtual and erect.
Object and image are equidistant from the mirror.
Principle of Reversibility of light
If the direction of a ray of light is reversed due to re§ection off a surface, then it will retrace its path.

Spherical Mirrors
Relationship between focus and radius of curvature
Focal length is half the distance between the pole and the radius of curvature.

Image formation by spherical mirrors
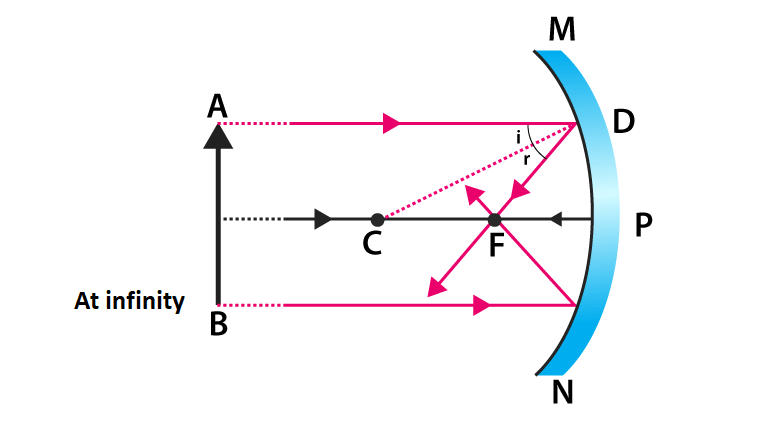
For objects at various positions, the image formed can be found using the ray diagrams for the special two rays. The following table is for a concave mirror.
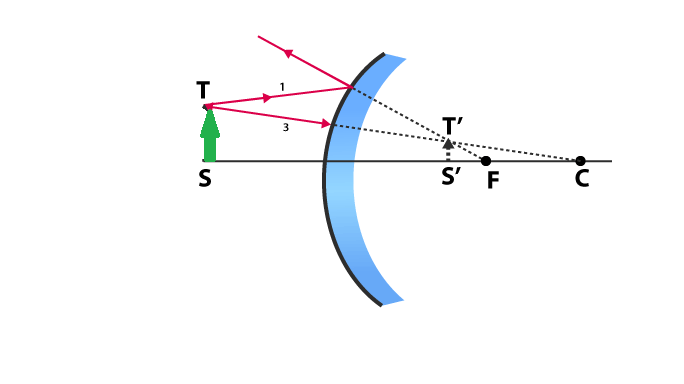
Concave Mirror Ray Diagram
Concave Mirror Ray Diagram lets us understand that, when an object is placed at infinity, a real image is formed at the focus. The size of the image is much smaller compared to that of the object.
When an object is placed behind the center of curvature, a real image is formed between the center of curvature and focus. The size of the image is smaller than compared to that of the object.

When an object is placed at the center of curvature and focus, the real image is formed at the center of curvature. The size of the image is the same as compared to that of the object.
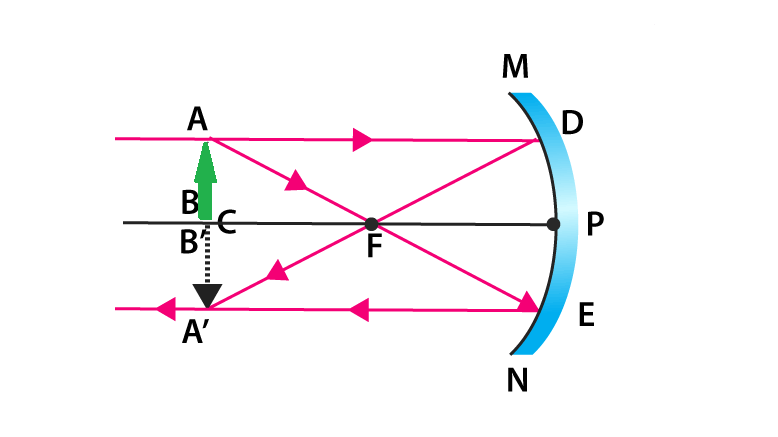
When an object is placed in between the center of curvature and focus, the real image is formed behind the center of curvature. The size of the image is larger than compared to that of the object.
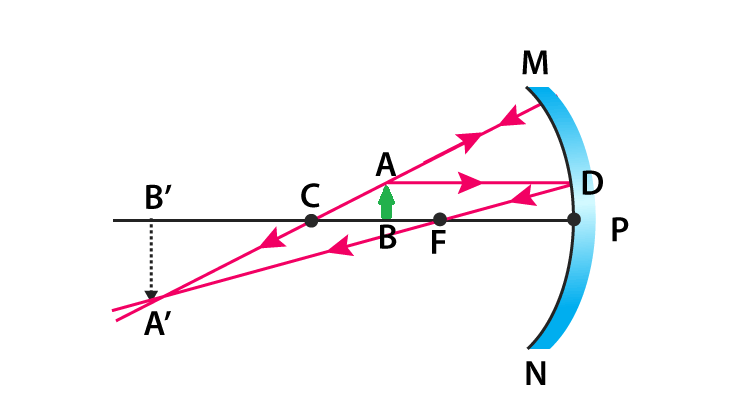
When an object is placed at the focus, the real image is formed at infinity. The size of the image is much larger than compared to that of the object.
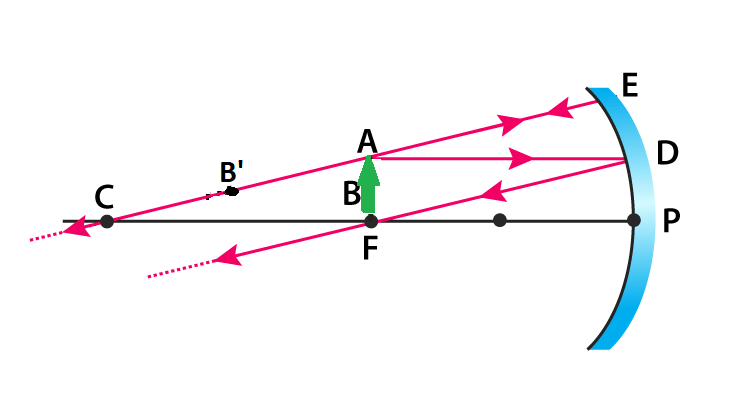
When an object is placed in between focus and pole, a virtual and erect image is formed. The size of the image is larger than compared to that of the object.
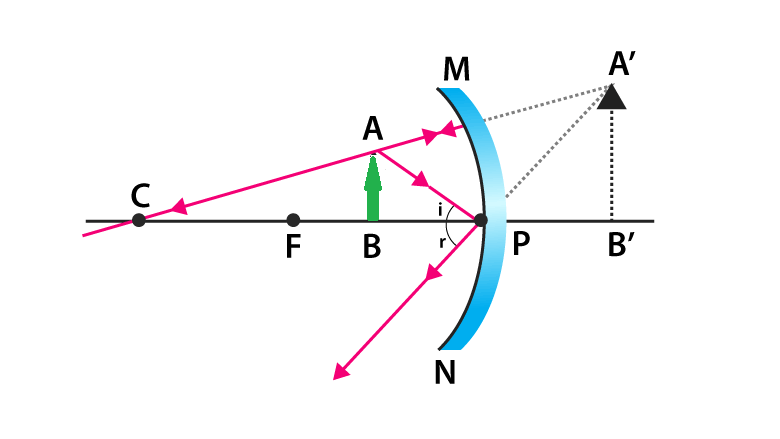
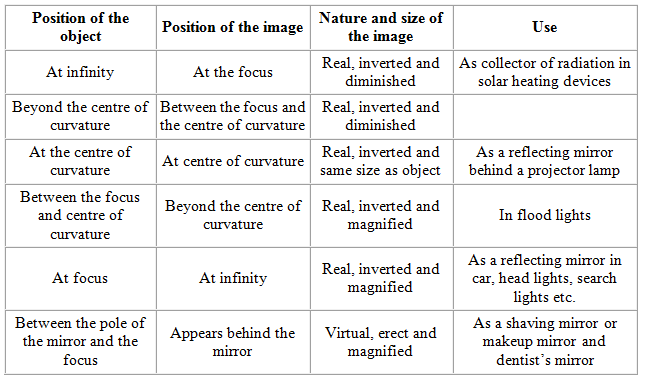
Image Formation By Convex Mirror
When an object is placed at infinity, a virtual image is formed at the focus. The size of the image is much smaller than compared to that of the object.

When an object is placed at a finite distance from the mirror, a virtual image is formed between the pole and the focus of the convex mirror. The size of the image is smaller than compared to that of the object.
Summary
| S. No | Position Of Object | Position of Image | Size of Image | Nature of Image |
| 1 | At Infinity | At the focus F, behind the mirror | Highly diminished | Virtual and Erect |
| 2 | Between Infinity and the Pole | Between P and F, behind the mirror | Diminished | Virtual and Erect |
Mirror Formula and Magnification
1/v + 1/u = 1/f where ‘u’ is object distance, ‘v’ is the image distance and ‘f’ is the focal length of a spherical mirror, which is found by the similarity of triangles.
The magnification produced by a spherical mirror is the ratio of the height of the image to the height of the object. It is usually represented as ‘m’.
Position and Size of image formed
Size of image can be found using the magni¦cation formula m = h’/h = – (v/u) If m is -ve it is a real image and if it is +ve it is a virtual image.
Refraction Through a Glass Slab and Refractive Index
Refraction
The shortest path need not be the quickest path. Since light is always in a hurry, it bends when it enters a different medium as it is still following the quickest path. This phenomenon of light bending in a different medium is called refraction.
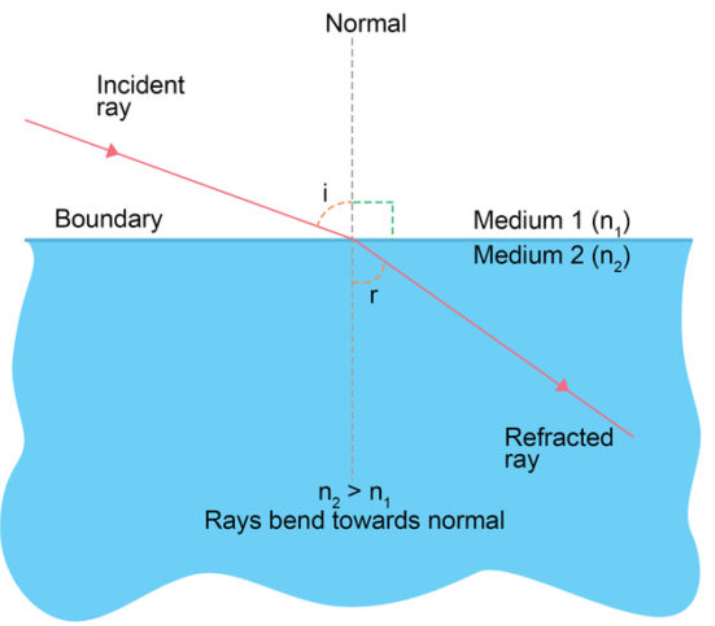
Laws of Refraction
- The incident ray, the refracted ray and the normal to the interface of two transparent media at the point of incidence, all lie in the same plane.
- The ratio of the sine of the angle of incidence to the sine of the angle of refraction is a constant, for the light of a given colour and for the given pair of media. This law is also known as Snell’s law of refraction.
Total internal reflection
- When the light goes from a denser to a rarer medium it bends away from the normal. The angle at which the incident ray causes the refracted ray to go along the surface of the two media parallelly is called critical angle.
- When the incident angle is greater than the critical angle, it reflects inside the denser medium instead of refracting. This phenomenon is known as Total Internal Reflection.
- E.g mirages, optical fibres.

Spherical Lens
Refraction at curved surfaces
When light is incident on a curved surface and passes through, the laws of refraction still hold true. For example lenses.
Spherical lenses
Spherical lenses are the lenses formed by binding two spherical transparent surfaces together. Spherical lenses formed by binding two spherical surfaces bulging outward are known as convex lenses while the spherical lenses formed by binding two spherical surfaces such that they are curved inward are known as concave lenses.
Important terms related to spherical lenses
- Pole (P): The midpoint or the symmetric centre of a spherical lens is known as its Optical Centre. It is also called as the pole.
- Principal Axis: The line passing through the optical centre and the centre of curvature.
- Paraxial Ray: A ray close to the principal axis and also parallel to it.
- Centre of curvature (C): The centres of the spheres that the spherical lens was a part of. A spherical lens has two centres of curvatures.
- Focus (F): It is the point on the axis of a lens to which parallel rays of light converge or from which they appear to diverge after refraction.
- Focal length: Distance between optical centre and focus.
- Concave lens: Diverging lens
- Convex lens: Converging lens
Rules of ray diagram for representation of images formed
- A ray of light parallel to principal axis passes/appears to pass through the focus.
- A ray passing through the optical centre undergoes zero deviation.
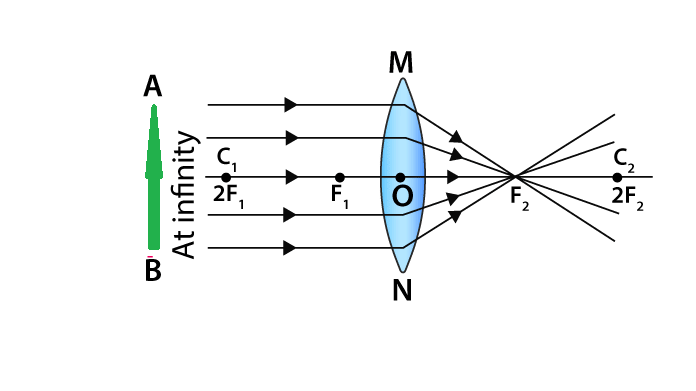
Convex Lenses
When an object is placed at infinity, the real image is formed at the focus. The size of the image is much smaller than that of the object.
When an object is placed behind the center of curvature, the real image is formed between the center of curvature and focus. The size of the image is the same as compared to that of the object.
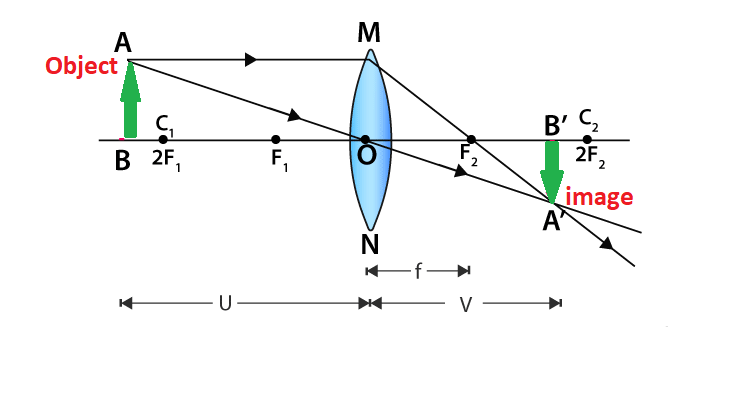
When an object is at the center of curvature, the real image is formed at the other center of curvature. The size of the image is the same as compared to that of the object.

When an object is placed in between the center of curvature and focus, the real image is formed behind the center of curvature. The size of the image is larger than that of the object.
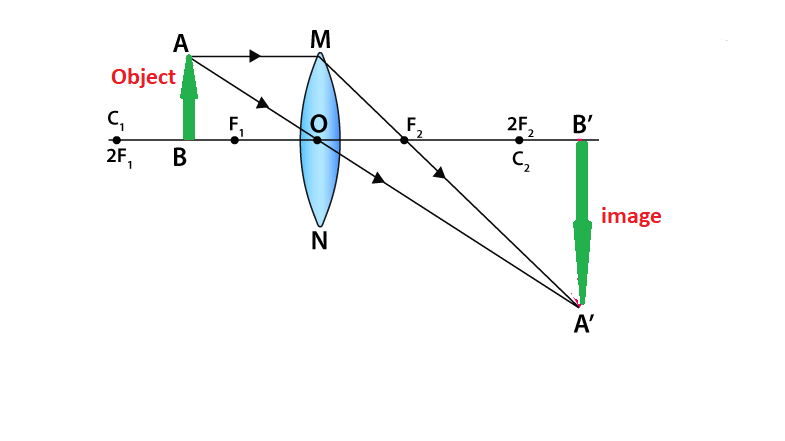
When an object is placed at the focus, a real image is formed at infinity. The size of the image is much larger than that of the object.

When an object is placed in between focus and pole, a virtual image is formed. The size of the image is larger than that of the object.

Concave Lenses
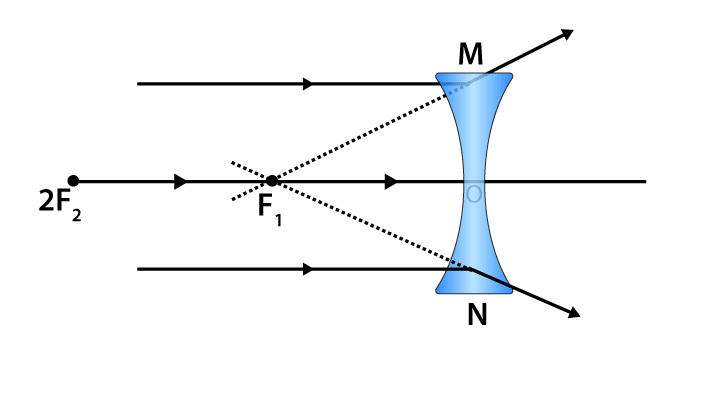
When an object is placed at infinity, a virtual image is formed at the focus. The size of the image is much smaller than that of the object.
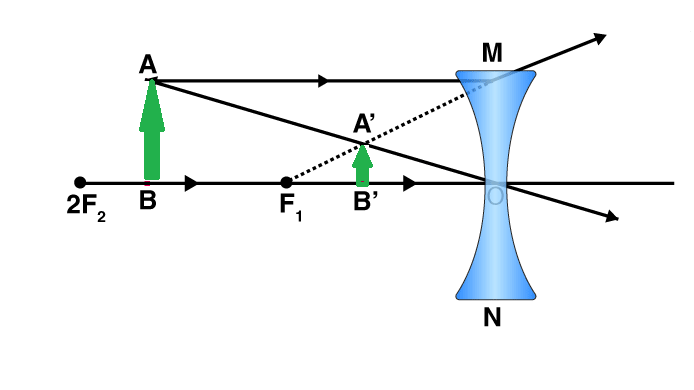
When an object is placed at a finite distance from the lens, a virtual image is formed between the pole and the focus of the convex lens. The size of the image is larger than that of the object.
Lens Formula, Magnification and Power of Lens
Lens formula and magnification
Lens formula: 1/v = 1/u = 1/f, gives the relationship between the object-distance (u), image-distance (v), and the focal length (f) of a spherical lens.
Uses of a spherical lens
Applications such as visual aids: spectacles, binoculars, magnifying lens, telescopes.
Power of a Lens
The power of a lens is the reciprocal of its focal length i.e 1/f (in metre). The SI unit of power of a lens is dioptre (D).