Q 1 – If AB || CD, EF ⊥ CD and ∠GED = 135° as per the figure given below.
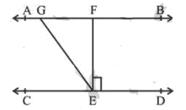
The value of ∠AGE is:
a) 120°
b) 140°
c) 90°
d) 135°
Ans. d) 135°
Q 2 – If AB = x + 3, BC = 2x and AC = 4x – 5, then for what value of ‘x’, B lies on AC?
a) 2
b) 3
c) 5
d) 8
Ans. d) 8
Q 3 – Value of x in the figure below is:
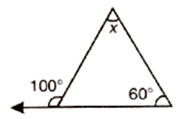
a) 20°
b) 40°
c) 80°
d) 160°
Ans. b) 40°
Q 4 – Two angles whose sum is equal to 180° are called:
a) Vertically opposite angles
b) Complementary angles
c) Adjacent angles
d) Supplementary angles
Ans. d) Supplementary angles
Q 5 – If two lines intersect each other, then the vertically opposite angles are:
a) Equal
b) Unequal
c) Cannot be determined
d) None of the above
Ans. a) Equal
Q 6 – In the given figure, if the angles a and b are in the ratio 2 : 3, then angle c is:
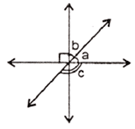
a) 90°
b) 126°
c) 144°
d) Obtuse angle
Ans. c) 144°
Q 7 – An acute angle is:
a) More than 90°
b) Less than 90°
c) Equal to 90°
d) Equal to 180°
Ans. b) Less than 90°
Q 8 – In the figure, p || q. The value of x is:
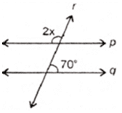
a) 35°
b) 55°
c) 70°
d) 110°
Ans. b) 55°
Q 9 – In figure, AB || ED, the value of x is:
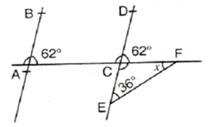
a) 26°
b) 36°
c) 54°
d) 62°
Ans. a) 26°
Q 10 – If an angle is half of its complementary angle, then find its degree measure.
Ans. Let the required angle be x
∴ Its complement = 90° – x
Now, according to given statement, we obtain x = (90° – x)
⇒ 2x= 90° – x
⇒ 3x = 90°
⇒ x = 30°
Hence, the required angle is 30°.
Q 11 – In the given figure, AB || CD, ∠FAE = 90°, ∠AFE = 40°, find ∠ECD.
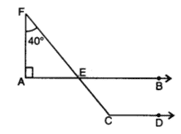
Ans. In ∆FAE,
ext. ∠FEB = ∠A + F
= 90° + 40° = 130°
Since AB || CD
∴ ∠ECD = FEB = 130°
Hence, ∠ECD = 130°.
Q 12 – In figure, if AB || CD. If ∠ABR = 45° and ∠ROD = 105°, then find ∠ODC.
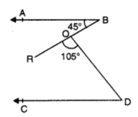
Ans.
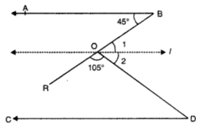
Through O, draw a line ‘l’ parallel to AB.
⇒ line I will also parallel to CD, then
∠1 = 45°[alternate int. angles]
∠1 + ∠2 + 105° = 180° [straight angle]
∠2 = 180° – 105° – 45°
⇒ ∠2 = 30°
Now, ∠ODC = ∠2 [alternate int. angles]
= ∠ODC = 30°
Q 13 – If AB || EF and EF || CD, then find the value of x.
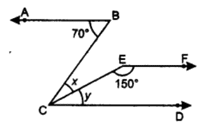
Ans. Since EF || CD ∴ y + 150° = 180°
⇒ y = 180° – 150° = 30°
Now, ∠BCD = ∠ABC
x + y = 70°
x + 30 = 70
⇒ x = 70° – 30° = 40°
Hence, the value of x is 40°
Q 14 – In Fig., POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR.
Prove that ∠ ROS = 1/2 (∠ QOS – ∠POS).
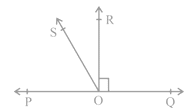
Ans.
POQ is a straight line. [Given]
∴ ∠POS + ∠ROS + ∠ROQ = 180°
But OR ⊥ PQ
∴ ∠ROQ = 90°
⇒ ∠POS + ∠ROS + 90° = 180°
⇒ ∠POS + ∠ROS = 90°
⇒ ∠ROS = 90° – ∠POS … (1)
Now, we have ∠ROS + ∠ROQ = ∠QOS
⇒ ∠ROS + 90° = ∠QOS
⇒ ∠ROS = ∠QOS – 90° ……(2)
Adding (1) and (2), we have
2 ∠ROS = (∠QOS – ∠POS)
∴ ∠ROS = 1/ 2(∠QOS−∠POS)
Q 15 – In the given figure, PQ || RS and EF || QS. If ∠PQS = 60°, then find the measure of ∠RFE.
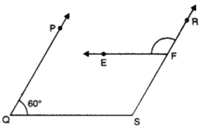
Ans.
Since PQ || RS
∴ ∠PQS + ∠QSR = 180°
⇒ 60° + ∠QSR = 180°
⇒ ∠QSR = 120°
Now, EF || QS ⇒ ∠RFE = ∠QSR [corresponding ∠s]
⇒ ∠RFE = 120°
Q 16 – If two parallel lines are intersected by a transversal, prove that the bisectors of two pairs of interior angles form a rectangle.
Ans. Given, AB || CD and transversal PQ meet these lines at E and F respectively.
EG and FH are the bisectors of pair of corresponding angles ∠PEB and ∠EFD.
To Prove,
EG || FH Proof
∵ EG and FH are bisectors of ∠PEB respectively.
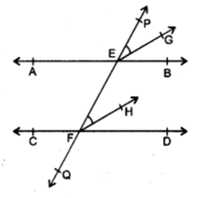
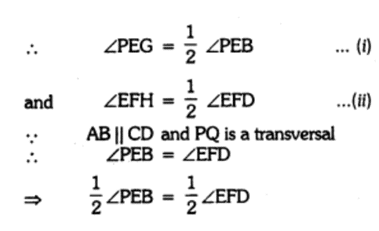
∠PEG = ∠EFH
Which are corresponding angles of EG and FH
∴ EG || FH.
Q 17 – In the figure, PS is the bisector of ∠QPR ; PT ⊥ RQ and Q > R. Show that
∠TPS = 1 /2 (∠Q – ∠R).
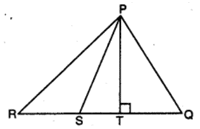
Ans. Since PS is the bisector of ∠QPR
∴ ∠QPS = ∠RPS = x (say)
In ∆ PRT, we have
∠PRT + ∠PTR + ∠RPT = 180°
⇒ ∠PRT + 90° + ∠RPT = 180°
⇒ ∠PRT + ∠RPS + ∠TPS = 90°
⇒ ∠PRT + 𝑥 + ∠TPS = 90°
⇒ ∠PRT or ∠R = 90° – ∠TPS – 𝑥
In ΔΡQT, we have
∠PQT + ∠PTQ + ∠QPT = 180°
⇒ ∠PQT + 90° + ∠QPT = 180°
⇒ ∠PQT + ∠QPS – TPS = 90°
⇒ ∠PQT + 𝑥 – ∠TPS = 90° [∵∠QPS = 𝑥]
⇒ ∠PQT or ∠Q = 90° + ∠TPS – 𝑥 ……(ii)
Subtracting (i) from (ii), we have
⇒ ∠Q – ∠R = (90° + ∠TPS – 𝑥) – 190° – ∠TPS – 𝑥)
⇒ ∠Q – ∠R = 90° + ∠TPS – 𝑥 – 90° + ∠TPS + 𝑥
⇒ 2 ∠TPS = 2Q – ∠R
⇒ ∠TPS = 1 / 2(Q – ∠R)
Q 18 – In Fig. 6.33, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror
RS at C and again reflects back along CD. Prove that AB || CD.
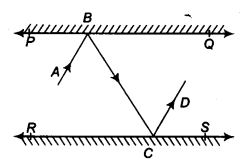
Ans. Draw ray BL ⊥PQ and CM ⊥ RS
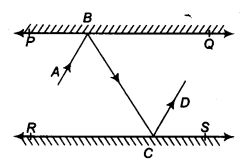
∵ PQ || RS ⇒ BL || CM
[∵ BL || PQ and CM || RS]
Now, BL || CM and BC is a transversal.
∴ ∠LBC = ∠MCB …(1) [Alternate interior angles]
Since angle of incidence = Angle of reflection
∠ABL = ∠LBC and ∠MCB = ∠MCD
⇒ ∠ABL = ∠MCD …(2) [By (1)]
Adding (1) and (2), we get
∠LBC + ∠ABL = ∠MCB + ∠MCD
⇒ ∠ABC = ∠BCD
i. e., a pair of alternate interior angles are equal.
∴ AB || CD
Class 9 Maths Lines and Angles Important Questions Download PDF File Here