Maths Combined MCQ test Set 1

Q 1 – There are 312, 260 and 156 students in class X, XI and XII respectively. Buses are to be hired to take these students to a picnic. Find the maximum number of students who can sit in a bus if each bus takes equal number of students.

(a) 52

(b) 56

(c) 48

(d) 63

Q 2 – Euclid’s Lemma states that, for given positive integers a and b, there exist unique integers q and r, such that a = bq + r, where :
(a) 0 < r < b
(b) 0 ≤ r < b
(c) 0 < r ≤ b
(d) 0 ≤ r ≤ b

Q 3 – HCF and LCM of two positive integers a and b satisfy a relationship, that:
(a) (HCF)(LCM) =
(b) (HCF) (LCM) = 1
(c) (HCF)(LCM) = ab
(d) No defined relation

Q 4 – The least number, which when divided by 10, 14 and 18, leaves remainder 4, is :
a) 630
(b) 634
(c) 252
(d) 496

Q 5 – The product of three consecutive positive integers is divisible by

(a) 4

(b) 6

(c) No comman factor

(d) Only

Q 6 – The HCF of a number which is neither prime nor composite and any other number x is:
(a) x
(b) x + 1
(c) 1
(d) Any number

Q 7 – The least number that is divisible by all the numbers from 1 to 8 (both inclusive) is
(a) 840
(b) 2520
(c) 8
(d) 420

Q 8 – A number when divided by 61 gives 27 as quotient and 32 as remainder. find the number
(a) 1967
(b) 1796
(c) 1679
(d) 1569

Q 9 – Two natural numbers whose difference is 66 and the least common multiple is 360, are:
(a) 120 and 54
(b) 90 and 24
(c) 180 and 114
(d) 130 and 64

Q 10 – A box contains cards numbered 6 to 50. A card is drawn at random from the box. The probability that the drawn card has a number which is a perfect square like 4,9….is
(a) 1/45
(b) 2/15
(c) 4/45
(d) 1/9

Q 11 – If α, s are the zeroes of x² – 8x + λ, such
that α – s = 2, then λ =
(a) 8
(b) 22
(c) 60
(d) 15

Q 12 – If LCM (77, 99) = 693, then HCF (77, 99) is

(a) 11

(b) 7

(c) 9

(d) 22

Q 13 – If α, s are the zeroes of p(x) = 2x² – 5x + 7, write a polynomial with zeroes 2α+3s and 3α+2s.
(a) k(x² + x – 41)
(b) k(x² – 25x + 41)
(c) k(x² – 20x – 41)
(d) k(- x² + 35x + 41)

Q 14 – Find the number of zeros in the graph given:

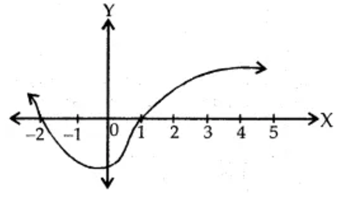
(a) 3
(b) 2
(c) 1
(d) 0

Q 15 – The product of two consecutive natural numbers is always:

a) prime number

b) even number

c) odd number

d) even or odd

Q 16 – 8 chairs and 5 tables cost Rs.10500, while 5 chairs and 3 tables cost Rs.6450. The cost of each chair will be
(a) Rs. 750
(b) Rs.600
(c) Rs. 850
(d) Rs. 900

Q 17 – The HCF of two numbers is 18 and their product is 12960. Their LCM will be
(a) 420
(b) 600
(c) 720
(d) 800

Q 18 – The zeroes of the quadratic polynomial x² + 1750x + 175000 are
(a) both negative
(b) one positive and one negative
(c) both positive
(d) both equal

Q 19 – If the zeroes of the quadratic polynomial x² + (a + 1) x + b are 2 and -3, then
(a) a = –7, b = –1
(b) a = 5, b = –1
(c) a = 2, b = –6
(d) a – 0, b = –6

Q 20 – If a and ß are the zeroes of the polynomial 5x² – 7x + 2, then sum of their reciprocals is:

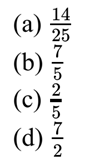
Q 21 – The zeroes of the quadratic polynomial x² + px + p, p ≠ 0 are
(a) both equal
(b) both cannot be positive
(c) both unequal
(d) both cannot be negative

Q 22 – The zeroes of the quadratic polynomial x² + 99x + 127 are
(a) both positive
(b) both negative
(c) one positive and one negative
(d) both equal

Q 23 – If  an  ordered  pair  satisfying  the  equations  2x−3y=18  and  4x−y=16  also  satisfies  the  equations 5x−Py−23=0, then find the value of P.

(a) –2
(b) 6
(c) 2
(d) 1

Q 24 – Find the dimensions of a garden, whose length is 4 m more than its width and half the perimeter is
36 m.
(a) 20 m × 16 m
(b) 14 m × 10 m
(c) 26 m × 22 m
(d) 12 m × 8 m

Q 25 – The sides of a triangle are AB, BC and AC whose equations are respectively y– 2 = 0; y = 3x – 7 and 2y + x = 0, The coordinates of points A and B are :
(a) A(3,2), B(–4,2)
(b) A(–4,2), B(3,2)
(c) A(3,2), B(2,–l)
(d) A(–4,2), B(2, –1)

Q 26 – Given is the system of Inconsistent equations, 2x + 7y = 11 and 5x + ky – 25 = 0, find k.

(b) 4

(d) – 4

Q 27 – In a AABC, ∠A = x°, ∠B = (3a – 2)° and ∠C = y°. Also, ∠C – ∠B = 9°. Find the value of ∠B.
(a) 73°
(b) 82°
(c) 25°
(d) 49°

Q 28 – An equation ax + by + c = 0 is a linear equation in 2 variables, where a, b, c are :
(a) natural numbers
(b) whole numbers
(c) integers
(d) real numbers

Q 29 – If x and y satisfy the given two equations, , ; find p is y = px – 2.
(a) 1
(b) 2
(c) 3

Q 30 – In a square of side 10 cm, its diagonal =

15 cm

10√2 cm

20 cm

12 cm

Q 31 – Find p and q so that given system has infinite number of solutions, 4x + 6y – 14 = 0. (p + q)x + (2 p – q)y – 3 (p + q +1) = 0
(a) p = 1, q = 1
(b) p = 1,q = – 1
(c) p = 1, q = 5
(d) p = 5, q = 1

Q 32 – If the distance between the points (x, –1) and (3, 2) is 5, then the value of x is

(a) –7 or –1
(b) –7 or 1
(c) 7 or 1
(d) 7 or –1

Q 33 – Find the values of x and y if ABCD is a cyclic quadrilateral, ∠A = 6x + 10°, ∠B = (5x)°, ∠C = (x + y)° (∠D)=(3y-10)°.
(a) x = 30°, y = 20°
(b) x = 20°, y = 30°
(c) x = 40°, y = 10°
(d) x = 10°, y = 40°

Q 34 – If x + 5y = 34 and x – 5y = – 6, find the value of 5y – 2x.
(a) – 8
(b) 14
(c) 8
(d) 20

Q 35 – One equation of a pair of dependent linear equations is – 5x + 7y = 2, the second equation can be :
(a) –10x + 14y + 4 = 0
(b) –10x – 14x + 4 = 0
(c) 10x – 14y = – 4
(d) 10x + 14y + 4 = 0

Q 36 – 8 girls and 12 boys can finish work in 10 days while 6 girls and 8 boys can finish it in 14 days. Find the time taken by the one girl alone that by one boy alone to finish the work.
(a) 120, 130
(b) 140,280
(c) 240,280
(d) 100,120

Q 37 – The graph of y = 4x is a line
(a) parallel to x-axis
(b) parallel to y-axis
(c) perpendicular to y-axis
(d) passing through the origin

Q 38 – The pair of equations 3x – 5y = 7 and – 6x + 10y = 7 have
(a) a unique solution
(b) infinitely many solutions
(c) no solution
(d) two solutions

Q 39 – The value of k, for which equations 3x + 5y = 0 and kx + y = 0 has a non-zero solution is
(a) 6
(b) 0
(c) 2
(d) 5

Q 40 – The present age of a father is the sum of the ages of his three sons. Ten years from now his age will be a three quarter of the sum of their ages then. How old is the father?
(a) 50 years
(b) 30 years
(c) 40 years
(d) 60 years

Q 41 – Which of the following pair of linear equations is inconsistent?
(a) 2x + 3y = 7; 4x + 6y = 5
(b) x – 2y = 6; 2x + 3y = 4
(c) 9x – 8y = 17; 18x -16y = 34
(d) 5x – 3y =11; 7x + 2y =13

Q 42 – Find the solution to the following system of linear equations:
2p+3q = 9 p – q = 2?
(a) (4,2)
(b) (3,1)
(c) (2,-3)
(d) (-4,1)

Q 43 – If x = a, y = b is the solution of the equations x + y = 5 and 2x – 3y = 4, then the values of a and b are respectively
(a) 6, –1
(b) 2, 3
(c) 1, 4

Q 44 – If A : Homogeneous system of linear equations is always consistent. R : x = 0, y = 0 is always a solution of the homogeneous system of equations with unknowns x and y, then which of the following statement is true?
(a) A is true and R is the correct explanation of A
(b) A is false and R is not a correrct explanation of A
(c) A is true and R is false
(d) A is false and R is true

Q 45 – Which geometric figures are always similar?
(a) Circles
(b) Circles and all regular polygons
(c) Circles and triangles
(d) Regular

Q 46 – ΔABC ~ ΔPQR, ∠B = 50° and ∠C = 70° then ∠P is equal to
(a) 50°
(b) 60°
(c) 40°
(d) 70°

Q 47 – In a rectangle Length = 8 cm, Breadth = 6 cm. Then its diagonal = …
(a) 9 cm
(b) 14 cm
(c) 10 cm
(d) 12 cm

Q 48 – The mid point of the line segment joining A(2a,4) and B(-2,3b) is M (1,2a + 1). The values of a and b are
(a) 2,3
(b) 1,1
(c) –2,–2
(d) 2,2

Q 49 – The line 3x + y – 9 = 0 divides the line joining the points (1, 3) and (2, 7) internally in the ratio
(a) 3 : 4
(b) 3 : 2
(c) 2 : 3
(d) 4 : 3

Q 50 – The ordinate of a point is twice its abscissa. If its distance from the point (4,3) is √10, then the coordinates of the point are
(a) (1,2) or (3,6)
(b) (1,2) or (3,5)
(c) (2,1) or (3,6)
(d) (2,1) or (6,3)

Q 51 – The perimeter of a triangle with vertices (0, 4) (0, 0) and (3, 0) is:
(a) 15
(b) 12
(c) 8
(d) 10

Q 52 – If (3,0), (2,a), and (b,6) are the vertices of ABC whose centroid is (2,5), then the values of a and b are
(a) a = 3, b = – 9
(b) a = 0, b = 2
(c) a = 1, b = 9
(d) a = 9, b = 1

Q 53 – If cos 9a = sin a and 9a < 90°, then the value of tan 5a is

(b) √3

(c) 1

(d) 0

Q 54 – 7 sin²θ + 3 cos²θ = 4 then :

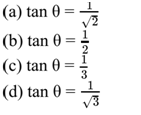
Q 55 – (1 + tanθ + secθ) (1 + cotθ – cosecθ) is equal to
(a) 0
(b) 1
(c) 2
(d) –1

Q 56 – In right triangle ABC, right angled at C, if tan A = 1, then the value of 2 sin A cos A is
(a) 0
(b) 1
(c) – 1
(d) 2

Q 57 – Given that sin A= and cos B= then the value of (A + B) is:
(a) 30°
(b) 45°
(c) 75°
(d) 15°

Q 58 – If sin θ + sin² θ = 1, then cos² θ + cos⁴ θ = ____
(a) -1
(b) 0
(c) 1
(d) 2

Q 59 – sin 2B = 2 sin B is true when B is equal to
(a) 90°
(b) 60°
(c) 30°
(d) 0°

Q 60 – If tan θ  + cot θ = 2, then tan²⁰ θ  + cot²⁰ θ =

(a) 0

(b) 2

(c) 20

(d) 2²⁰

Q 61 – The perimeter of a circle is equal to that of a square, then the ratio of their areas is
(a) 22 : 7
(b) 14 : 11
(c) 1 : 22
(d) 11 : 14

Q 62 – The ratio of area of two circles whose ratio of circumference is 3:1 will be
(a) 3 : 1
(b) 1 : 3
(c) 1 : 9
(d) 9 : 1

Q 63 – The area of a circle whose circumference is 22 cm, is
(a) π cm²
(b) 38.5 cm²
(c) 22 cm²
(d) 77 cm²

Q 64 – The circumference of two concentric circles forming a ring are 88 cm and 66 cm. Taking  = 22/7, the width of the ring is

(a) 14 cm

(b) 7 cm

(c) 7/2 cm

(d) 21 cm

Q 65 – It is proposed to build a single circular park equal in area to the sum of areas of two circular parks of diameters 16 m and 12 m in a locality. The radius of the new park would be
(a) 10 m
(b) 15 m
(c) 20 m
(d) 24 m

Q 66 – The diameter of a wheel is 1.26 m. The distance travelled in 500 revolutions is
(a) 2670 m
(b) 2880 m
(c) 1980 m
(d) 1596 m

Q 67 – If the radius of a circle is doubled, its area becomes

(a) 2 times

(b) 4 times

(c) 8 times

(d) 16 times

Q 68 – The area of the square that can be inscribed in a circle of radius 12 cm is
(a) 288 sq. cm
(b) 576 sq. cm
(c) 144 sq.cm
(d) 500 sq. cm

Q 69 – The radii of two circles are 4 cm and 3 cm respectively. The diameter of the circle having area equal to the sum of the areas of the two circles (in cm) is:
(a) 5
(b) 7
(c) 10
(d) 14

Q 70 – The radii of two circles are 19 cm and 9 cm respectively. The radius of the circle which has circumference equal to the sum of the circumference of two circles is
(a) 35 cm
(b) 10 cm
(c) 21 cm
(d) 28 cm

Q 71 – Which of the following is true –
(a) Mode = 3Median + 2Mean

Q 72 – The perimeters of two similar triangles are 26 cm and 39 cm. The ratio of their areas will be
(a) 2:3
(b) 6:9
(c) 4:6
(d) 4:9

Q 73 – The wickets taken by a bowler in 10 cricket matches are 2, 6, 4, 5, 0, 3, 1, 3, 2, 3. The mode of the data is
(a) 1
(b) 2
(c) 3
(d) 4

Q 74 – The median of first 10 prime numbers is
(a) 11
(b) 12
(c) 13
(d) none of these

Q 75 – A vertical stick 20m long casts a shadow 10m long on the ground. At the same time a tower casts a shadow 50m long. What is the height of the tower?
(a) 30m
(b) 50m
(c) 80m
(d) 100m

Q 76 – The mean and the median of a distribution are 45.9 and 46 respectively. The mode will be
(a) 45
(b) 47
(c) 48
(d) 46.2

Q 77 – While computing mean of grouped data, we assume that the frequencies are
(a) evenly distributed over all the classes
(b) centred at the classmarks of the classes
(c) centred at the upper limits of the classes
(d) centred at the lower limits of the classes

Q 78 – The age of 18 students of a class is reported below. Their modal age is 10, 17, 14, 10, 11, 12, 12, 13, 17, 13, 14, 14, 15, 16, 17, 15, 17, 16
(a) 22 years
(b) 17 years
(c) 14 years
(d) 16 years

Q 79 – Which of the following cannot be determined graphically?
(a) Mean
(b) Median
(c) Mode
(d) None of these

Q 80 – Two congruent triangles are actually similar triangles with the ratio of corresponding sides as.
(a) 1:2
(b) 1:1
(c) 1:3
(d) 2:1

Download Answers Class 10 Maths Combined Paper Set I