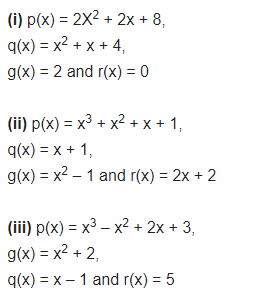NCERT SOLUTIONS FOR CLASS 10 MATHS CHAPTER 2 POLYNOMIALS EX -2.3

Question 1. Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following:
(i) p(x) = x³ – 3x² + 5x – 3, g(x) = x² – 2
(ii) p(x) = x⁴ – 3x² + 4x + 5, g(x) = x² + 1 – x
(iii) p(x) = x⁴– 5x + 6, g(x) = 2 – x²
Solution:

(i) p(x) = x³ – 3x² + 5x – 3, g(x) = x² – 2 dividing p(x) by g(x)

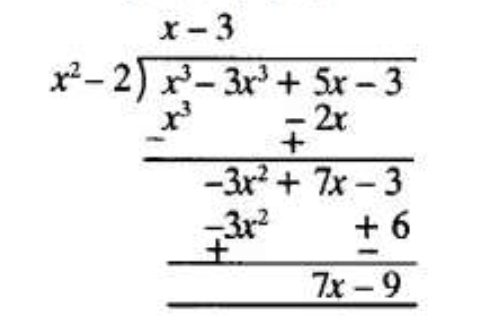
Quotient = x – 3, Remainder = 7x – 9

(ii) p(x) = x⁴ – 3x² + 4x + 5, g(x) = x² + 1 – x dividing p(x) by g(x)

Quotient = x² + x – 3, Remainder = 8

(iii) p(x) = x⁴– 5x + 6, g(x) = 2 – x²

Rearranging g(x) = –x² + 2 dividing p(x) by g(x)

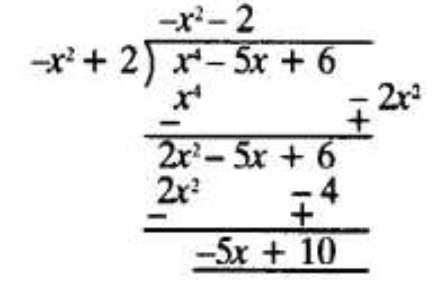
Quotient = – x² – 2, Remainder = –5x + 10

Question 2.
Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial.
(i) t² – 3, 2t⁴ + 3t³ – 2t²– 9t – 12
(ii) x² + 3x + 1, 3x⁴ + 5x³ – 7x² + 2x + 2
(iii) x² + 3x + 1, x⁵ – 4x³ + x² + 3x + 1
Solution:

(i) First Polynomial = t² – 3,

Second Polynomial = 2t⁴ + 3t³ – 2t²– 9t – 12

dividing second polynomial by first polynomial.

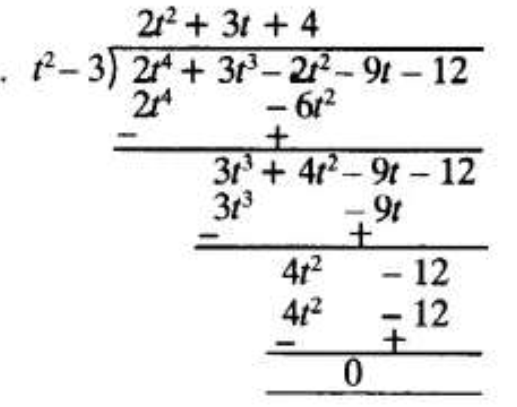
Remainder is Zero, First polynomial is a factor of second polynomial.

(ii) x² + 3x + 1, 3x⁴ + 5x³ – 7x² + 2x + 2

First Polynomial = x² + 3x + 1

Second Polynomial = 3x⁴ + 5x³ – 7x² + 2x + 2

dividing second polynomial by first polynomial.

Remainder is Zero, First polynomial is a factor of second polynomial.

CLASS 10 MATHS POLYNOMIALS Ex 2.3 Solutions

(iii) x² + 3x + 1, x⁵ – 4x³ + x² + 3x + 1

First Polynomial = x² + 3x + 1

Second Polynomial = x⁵ – 4x³ + x² + 3x + 1

dividing second polynomial by first polynomial.

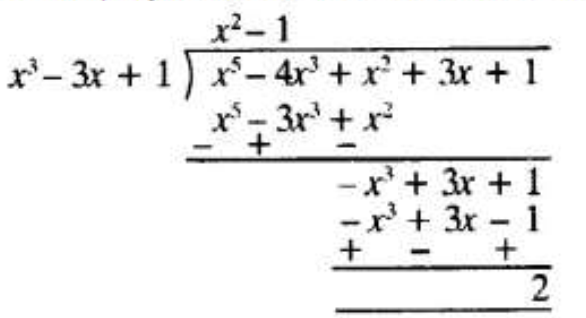
Remainder ≠ 0

First Polynomial is not a factor of second polynomial.

Question 3. Obtain all other zeroes of 3x⁴ + 6x³ – 2x² – 10x – 5, if two of its zeroes are  and √(5/3) and −√(5/3)
Solution:

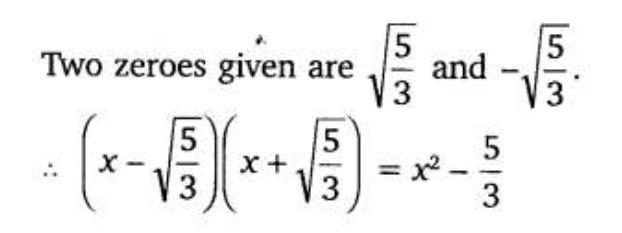
= 1/3 x (3x² – 5) Since both 1/3 and (3x² – 5) are the factors, therefore 3x² – 5 is a factor of the given polynomial.

Now, we divide the given polynomial by 3x² – 5

Hence, the other zeroes of the given polynomial are –1 and –1.

CLASS 10 MATHS POLYNOMIALS Ex 2.3 Solutions

Question 4. On dividing x³ – 3x² + x + 2 by a polynomial g(x), the quotient and remainder were x – 2 and –2x + 4 respectively. Find g(x).
Solution:

p(x) = x³ – 3x² + x + 2 ,

g(x) = ?

Quotient = x – 2; Remainder = – 2x + 4

On dividing p(x) by g(x), we have

p(x) = g(x) x quotient + remainder as per Euclid’s Division Lemma

⟹ x³ – 3x² + x + 2 = g(x) (x – 2) + (–2x + 4)

⟹ x³ – 3x² + x + 2 + 2x – 4 = g(x) x (x – 2)

⟹ x³ – 3x² + 3x – 2 = g(x) x (x – 2)

⟹ g(x) = x³ – 3x² + 3x – 2 / (x – 2)

⟹ g(x) = x² – x + 1

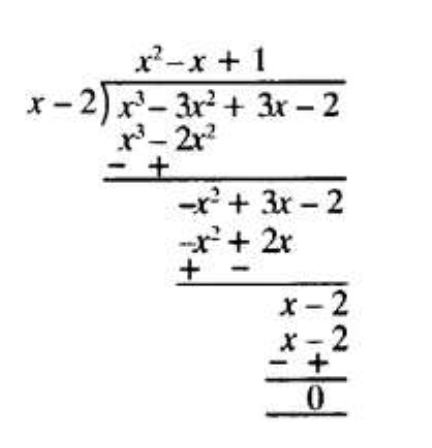
Question 5.
Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and:
(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg r(x) = 0
Solution: