NCERT SOLUTIONS FOR CLASS 10 MATHS QUADRATIC EQUATIONS CHAPTER 4 EX 4.1
Question 1. Check whether the following are quadratic equations:
(i) (x+ 1)2 = 2 (x-3)
(ii) x – 2x = (- 2) (3 – x)
(iii) (x – 2) (x + 1) = (x – 1) (x + 3)
(iv) (x – 3) (2x + 1) = x (x + 5)
(v) (2x – 1) (x – 3) = (x + 5) (x – 1)
(vi) x2 + 3x + 1 = (x – 2)2
(vii) (x + 2)3 = 2x(x2 – 1)
(viii) x3 – 4x2 – x + 1 = (x – 2)3
Solution:

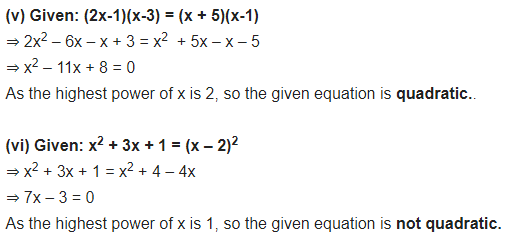
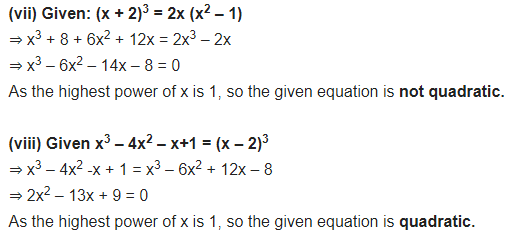
Question 2. Represent the following situations in the form of quadratic equations:
(i) The area of a rectangular plot is 528 m2. The length of the plot (in metres) is one more than twice its breadth. We need to find the length and breadth of the plot.
(ii) The product of two consecutive positive integers is 306. We need to find the integers.
(iii) Rohan’s mother is 26 years older than him. The product of their ages (in years) 3 years from now will be 360. We would like to find Rohan’s present age.
(iv) A train travels a distance of 480 km at a uniform speed. If the speed had been 8 km/h less, then it would have taken 3 hours more to cover the same distance. We need to find the speed of the train.
Solution:


Quadratic Equation
The standard form of the quadratic equation in the variable x is an equation of the form ax2 + bx + c = 0, where a, b, c are real numbers and a ≠ 0.
Any equation of the form P(x) = 0, Where P(x) is a polynomial of degree 2, is a quadratic equation.
Zero(es)/Root(s) of Quadratic Equation
A real number α is said to be a root of the quadratic equation ax2 + bx + c = 0, a ≠ 0 if aα2 + bα + c = 0.
We can say that x = α, is a solution of the quadratic equation or that α satisfies the quadratic equation.
The zeroes of the quadratic polynomial ax2 + bx + c = 0 and the roots of the equation ax2 + bx + c = 0 are same. A quadratic equation has atmost two roots/zeroes.
Relation Between Zeroes and Co-efficient of a Quadratic Equation
If α and β are zeroes of the quadratic equation ax2 + bx + c = 0, where a, b, c are real numbers and a ≠ 0 then

Methods of Solving Quadratic Equation
Following are the methods which are used to solve quadratic equations:
(i) Factorisation
(ii) Completing the square
(iii) Quadratic Formula
Methods of Factorisation
In this method we find the roots of a quadratic equation (ax2 + bx + c = 0) by factorising LHS it into two linear factors and equating each factor to zero, e.g.,
6x2 – x – 2 = 0
⇒ 6x2 + 3x – 4x – 2 = 0 …(i)
⇒ 3x (2x + 1) – 2(2x + 1) = 0
⇒ (3x — 2) (2x + 1) = 0
⇒ 3x – 2 = 0 or 2x + 1 = 0
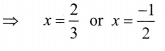
Necessary Condition: Product of 1st and last terms of eq. (i) should be equal to the product of 2nd and 3rd terms of the same equation.
Method of Completing the Square
This is the method of converting L.H.S. of a quadratic equation which is not a perfect square into the sum or difference of a perfect square and a constant by adding and subtracting the suitable constant terms. E.g,
(1) x2 + 4x – 5 = 0
⇒ x2 + 2(2) (x) -5 = 0
⇒ x2 + 2(2) (x) + (2)2 – (2)2 – 5 = 0
⇒ (x + 2)2 – 4 – 5 = 0
⇒ (x + 2)2 – 9 = 0
⇒ x + 2 = ± 3
⇒ x = —5, 1
(2) 3x2 – 5x + 2 = 0
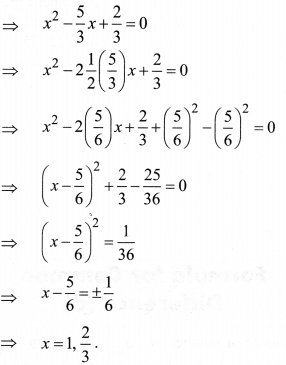
Quadratic Formula
Consider a quadratic equation: ax2 + bx + c = 0.
If b2 – 4ac ≥ 0, then the roots of the above equation are given by:
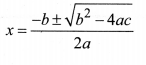
Nature of Roots
For quadratic equation ax2 + bx + c = 0
(a ≠ 0), value of (b2 – 4ac) is called discriminant of the equation and denoted as D.
D = b2 – 4ac
Discriminant is very important in finding nature of the roots.
(i) If D = 0, then roots are real and equal.
(ii) If D > 0, then roots are real and unequal
(iii) If D < 0, then roots are not real.