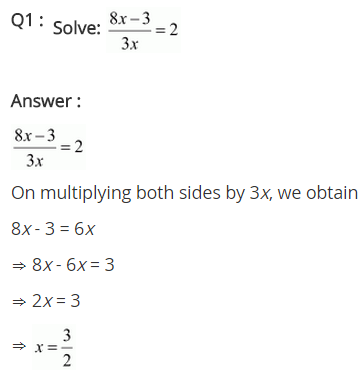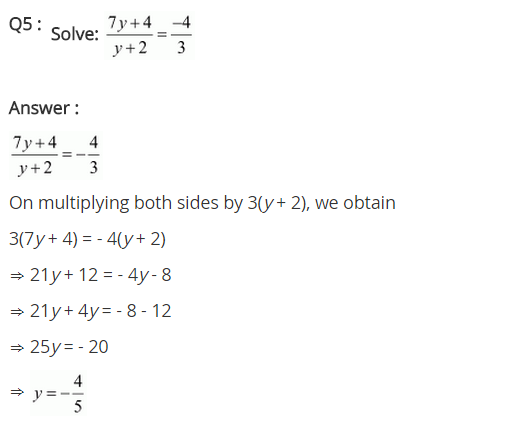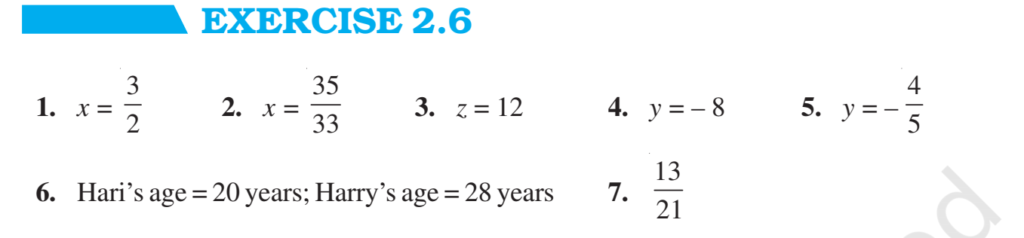Solve the following equations.
Question 1.
8x−3 / 3x=2
Solution:
We have 8x−3 / 3x=2
⇒ 8x−3 / 3x = 2/1
⇒ 8x – 3 = 2 × 3x (Cross-multiplication)
⇒ 8x – 3 = 6x
⇒ 8x – 6x = 3 (Transposing 6x to LHS and 3 to RHS)
⇒ 2x = 3
⇒ x = 3 / 2
Question 2.
9x / 7−6x = 15
Solution:
we have 9x / 7−6x = 1/5
⇒ 9x / 7−6x = 15/ 1
⇒ 9x = 15(7 – 6x) (Cross-multiplication)
⇒ 9x = 105 – 90x (Solving the bracket)
⇒ 9x + 90x = 105 (Transposing 90x to LHS)
⇒ 99x = 105
⇒ x = 105 / 99
⇒ x = 35 / 33
Question 3.
z / z+15=4 /9
Solution:
We have z / z+15=4 / 9
⇒ 9z = 4 (z + 15) (Cross-multiplication)
⇒ 9z = 4z + 60 (Solving the bracket)
⇒ 9z – 42 = 60
⇒ 5z = 60
⇒ z = 12
Ex 2.6 Class 8 Maths Question 4.
3y+4 / 2−6y=−25
Solution:
we have 3y+4 / 2−6y=−2 / 5
⇒ 5(3y + 4) = -2(2 – 6y) (Cross-multiplication)
⇒ 15y + 20 = -4 + 12y (Solving the bracket)
⇒ 15y – 12y = -4 – 20 (Transposing 12y to LHS and 20 to RHS)
⇒ 3y = -24 (Transposing 3 to RHS) -24
⇒ y = -8
Question 5.
7y+4 / y+2=−4 / 3
Solution:
we have 7y+4 / y+2=−4 / 3
⇒ 3(7y + 4) = -4 (y + 2) (Corss-multiplication)
⇒ 21y + 12 = -4y – 8 [Solving the bracket]
⇒ 21y + 4y = -12 – 8 [Transposing 4y to LHS and 12 to RHS]
⇒ 25y = -20 [Transposing 25 to RHS]
⇒ y = −4 / 5
Question 6.
The ages of Hari and Harry are in the ratio 5 : 7. Four years from now the ratio of their ages will be 3 : 4. Find their present ages.
Solution:
Let the present ages of Hari and Harry be 5x years and 7x years respectively.
After 4 years Hari’s age will be (5x + 4) years and Harry’s age will be (7x + 4) years.
As per the conditions, we have
5x+4 / 7x+4 = 3 / 4
⇒ 4(5x + 4) = 3(7x + 4) (Cross-multiplication)
⇒ 20x + 16 = 21x + 12 (Solving the bracket)
⇒ 20x – 21x = 12 – 16 (Transposing 21x to LHS and 16 to RHS)
⇒ -x = -4
⇒ x = 4
Hence the present ages of Hari and Harry are 5 × 4 = 20years and 7 × 4 = 28years respectively.
Question 7.
The denominator of a rational number is greater than its numerator by 8. If the numerator is increased by 17 and the denominator is decreased by 1, the number obtained is 32. Find the rational number.
Solution:
Let the numerator of the rational number be x.
Denominator = (x + 8)
As per the conditions, we have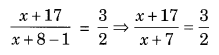
⇒ 2(x + 17) = 3(x + 7) (Cross-multiplication)
⇒ 2x + 34 = 3x + 21 (Solving the bracket)
⇒ 2x – 3x = 21 – 34 (Transposing 3x to LHS and 34 to RHS)
⇒ -x = -13
⇒ x = 13
Thus, numerator = 13
and denominator = 13 + 8 = 21
Hence the rational number is 13 / 21.