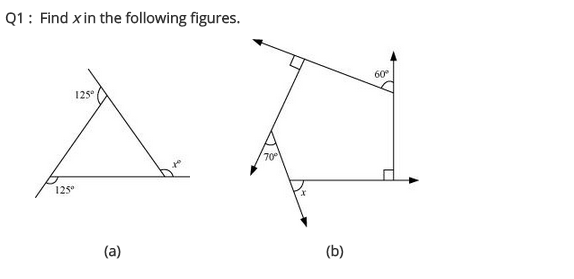
Question 1.
Find x in the following figures.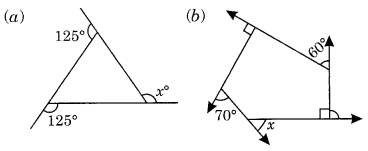
Solution:
(a) We know that the sum of all the exterior angles of a polygon = 360°
125° + 125° + x = 360°
⇒ 250° + x = 360°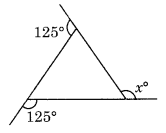
x = 360° – 250° = 110°
Hence x = 110°
(b) Here ∠y = 180° – 90° = 90°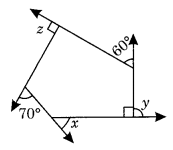
and ∠z = 90° (given)
x + y + 60° + z + 70° = 360° [∵ Sum of all the exterior angles of a polygon = 360°]
⇒ x + 90° + 60° + 90° + 70° = 360°
⇒ x + 310° = 360°
⇒ x = 360° – 310° = 50°
Hence x = 50°
Question 2.
Find the measure of each exterior angle of a regular polygon of
(i) 9 sides
(ii) 15 sides
Solution:
(i) We know the sum of all the exterior angles of polygon = 360°
Measure of each angle of 9 sided regular polygon = 3609 = 40°
(ii) Sum of all the exterior angles of a polygon = 360°
Measure of each angle of 15 sided regular polygon = 36015 = 24°
Question 3.
How many sides does a regular polygon have if the measure of an exterior angle is 24°?
Solution:
Sum of all exterior angles of a regular polygon = 360°
Number of sides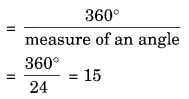
Hence, the number of sides = 15
Question 4.
How many sides does a regular polygon have if each of its interior angles is 165°?
Solution:
Let re be the number of sides of a regular polygon.
Sum of all interior angles = (n – 2) × 180°
and, measure of its each angle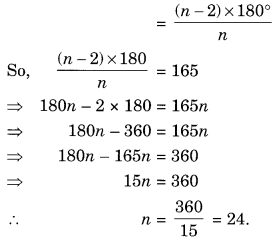
Hence, the number of sides = 24
Question 5.
(a) Is it possible to have a regular polygon with measure of each exterior angle a is 22°?
(b) Can it be an interior angle of a regular polygon? Why?
Solution:
(a) Since, the sum of all the exterior angles of a regular polygon = 360° which is not divisible by 22°.
It is not possible that a regular polygon must have its exterior angle 22°.
(b) Sum of all interior angles of a regular polygon of side n = (n – 2) × 180°
not a whole number.
Since number of sides cannot be in fractions.
It is not possible for a regular polygon to have its interior angle = 22°.
Question 6.
(a) What is the minimum interior angle possible for a regular polygon? Why?
(b) What is the maximum exterior angle possible for a regular polygon?
Solution:
(a) Sum of all interior angles of a regular polygon of side n = (n – 2) × 180°
The measure of each interior angle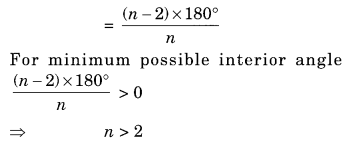
The minimum measure the angle of an equilateral triangle (n = 3) = 60°.
(b) From part (a) we can conclude that the maximum exterior angle of a regular polygon = 180° – 60° = 120°.