Polynomial Class 9 important Questions Maths Chapter 2 -

Q 1 – Find the products:

(i) (𝑥 – 1) (𝑥 + 1) (𝑥²+ 1) (𝑥⁴ + 1)

(ii)( $x-\frac{1}{2}$ ) ( $x+\frac{1}{x}$ ) ( $x^{2}+\frac{1}{x^2}$ ) ( $x^{4}+\frac{1}{x^4}$ )

Ans. (i)

= (x -1) (x +1) (x² +1) (x⁴ +1)

= (x²-1)(x²+1)(x⁴ +1)

={(x²)²-1²}(x⁴+1)

=(x⁴ —1)( x⁴ +1) = (x⁴ )² —1² = x⁸ —1

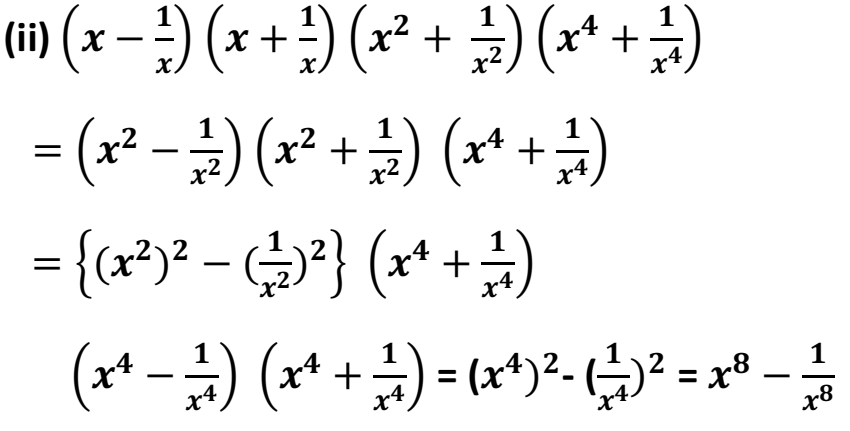
(ii)( $x-\frac{1}{2}$ ) ( $x+\frac{1}{x}$ ) ( $x^{2}+\frac{1}{x^2}$ ) ( $x^{4}+\frac{1}{x^4}$ )

Q 2 – Prove that:

a³ + b³ + c³ – 3abc = $\frac{1}{2}$ (a + b + c) {(a – b)² + (b – c)² + (c – a)²}

Ans.

We have,

a³ + b³ + c³ – 3abc

= (a + b + c)(a² +b² +c² – ab – bc – ca)

$=\frac{1}{2}$ (a + b + c)(2a² + 2b² + 2c² – 2ab – 2bc – 2ca)

$=\frac{1}{2}$ (a + b + c){(a² – 2ab + b² ) + (b² – 2bc + c² ) + (c² – 2ca + a²)}

$=\frac{1}{2}$ (a + b + c) { (a – b)² + (b – c)² + (c – a)²}

Q 3 – If 4^𝑥 – 4^𝑥-1= 24, then (2𝑥)^𝑥 equals ………

Ans.

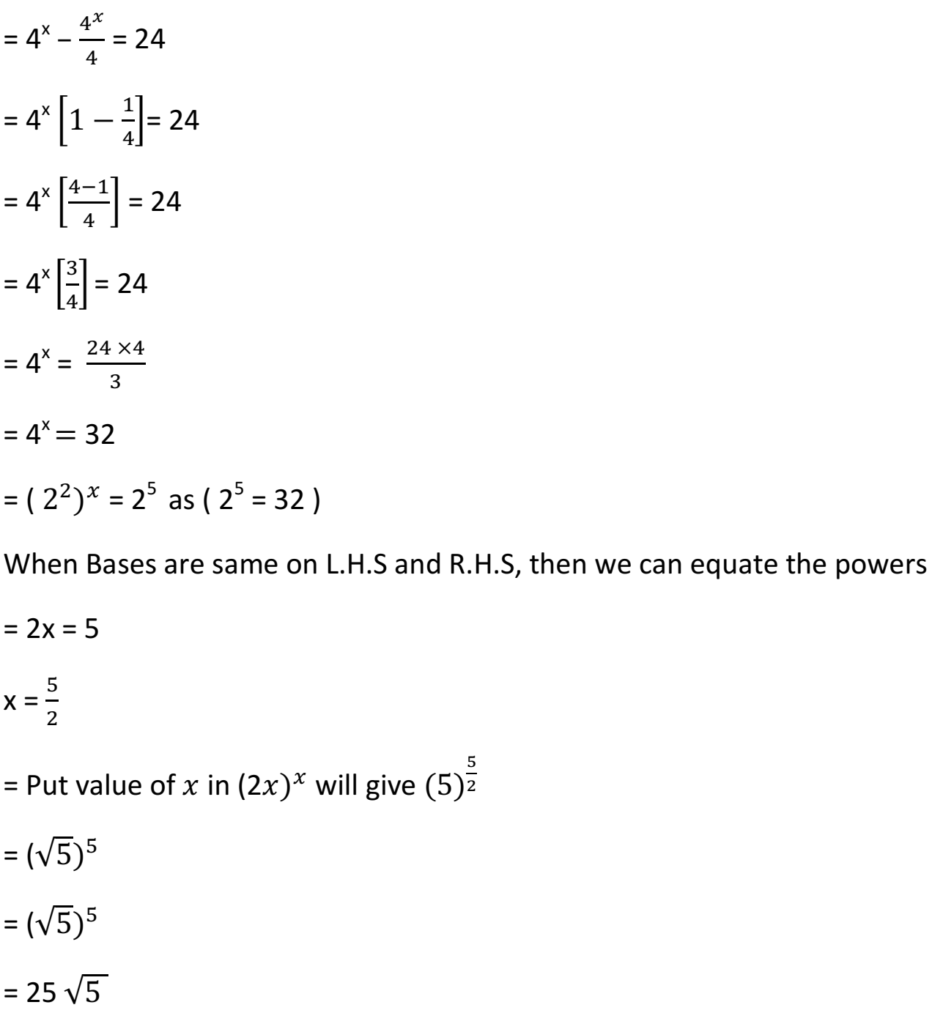
Q 4 – If a + b = 10 and a² + b² = 58, find the value of a³ + b³

Ans.

(a+b)² = a²+b²+2ab.
(10)²=58+2ab
$ab= \frac{(100- 58)}{2}$
$ab= \frac{42}{2}=21$
now,
(a+b)³=a³+b³+3ab(a+b)
10³=a³+b³+(3 × 21 ×10)
a³+b³=1000-630
therefore, a³+b³=370.

Q 5 – Show that:

p – 1 is a factor of p¹⁰ + p⁸ + p⁶ – p⁴ – p² – 1.

Ans.

p – 1= 0
p = 1
on putting an equation p =1
(1) × 10 + (1) × 8 + (1) × 6 – (1) × 4 – (1) × 2 – 1
10 + 8 + 6 – 4 –2 –1 =18 + 6 – 6 –1 =18 –1 =17
no it is not factor.

Q 6 – Prove that:

(a + b)³ + (b + c)³ + (c + a)³ – 3(a + b)(b + c)(c + a) = 2(a³ + b³+ c³ – 3abc)

Ans.

Solve L.H.S:

L.H.S =(b+c)³+(c+a)³+(a+b)³−3(b+c)(c+a)(a+b)

Using algebraic formula,

(a+b)³=a³+3a²b+3ab²+b³

=b³+c³+3b²c+3bc²+c³+a³+3c²a+3ca²

= a³+b³+3a²b+3ab²−3(b+ c) (c+a)(a+b)

=2(a³+b³+c³)+3b²c+3bc²+3c²a+3ca²+3a²b+3ab²−3(b+c) (c + a) (a+b)+6abc−6abc

=2(a³+b³+c³)+3b²c+3bc²+3c²a+3ca²+3a²b+3ab²−3(b+c)(c + a) (a+b)−6abc

=2(a³+b³+c³)+3(b+c)(c+a)(a+b)−3(b+c)(c+a)(a+b)−6abc

=2(a3+b3+c3)−6abc

=2(a³+b³+c³−3abc)

=R.H.S, Hence proved.

Q 7 – If a + b + c = 0 then write the value of $\frac{a^2}{bc}$ + $\frac{b^2}{ca}$ + $\frac{c^2}{ab}$

Q 8 – Factorize: 2√2𝑥³ + 3√3𝑦³ + √5 (5 – 3√6𝑥𝑦)

Ans. Instruction Based on

a³+b³+c³−3abc formula

Calculation

2√2x3+3√3y3+√5(5−3√6xy)

2√2x3+3√3y3+5√5−3√6×√5xy

(√2x+√3y+√5)(2×2+3y2+52−√6xy−√15y−√10x)

Q 9 – The product (a + b) (a – b) (a² – ab + b²) (a² + ab + b²) is equal to

Ans.

= (a + b)(a – b)(a² – ab + b²)(a² + ab + b²)

= (a + b)(a² – ab + b²) × (a – b)(a² + ab + b²)

= (a³ + b³) × (a³ – b³)

= (a³)² – (b³)²

= a⁶ – b⁶

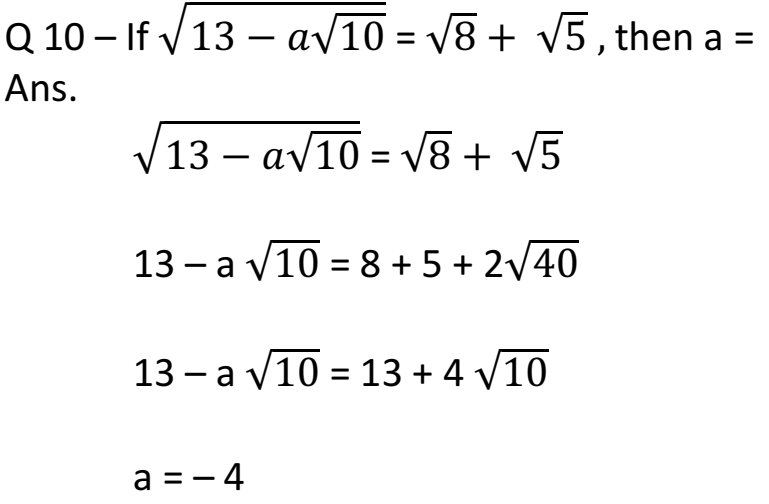
Q 11 – Simplify:

**$\frac{16 * 2^{n+1}-42^n}{16 2^{n+2}-2*2^{n+2}}$**

Ans.

Q 12 – If a² + b² + c² – ab – bc – ca = 0, prove that a = b = c.

Ans.

Consider, a² + b² + c² – ab – bc – ca = 0

Multiply both sides with 2, we get

2( a² + b² + c² – ab – bc – ca) = 0

2a² + 2b² + 2c² – 2ab – 2bc – 2ca = 0

(a² – 2ab + b²) + (b² – 2bc + c²) + (c² – 2ca + a²) = 0

(a –b)² + (b – c)² + (c – a)² = 0

Since the sum of the square is zero then each term should be zero

(a –b)² = 0, (b – c)² = 0, (c – a)² = 0

(a –b) = 0, (b – c) = 0, (c – a) = 0

a = b, b = c, c = a

∴ a = b = c

Q 13 – Find the value of k, (𝑥 + 𝑦)³ – (𝑥 – 𝑦)³– 6𝑦(𝑥² – 𝑦²) = k𝑦²

Ans.

( x + y)³ -( x -y)³ -6y(x² – y² ) = Ky²

we know,
a³ – b³ = (a – b)( a² + ab + b²)

(x + y)³ -(x – y)³ = (x + y – x + y){(x +y)² + ( x -y)² + (x +y)(x -y) }

=( 2y ) { 2x² + 2y² + x² – y²)

= 2y ( 3x² + y²)

put this in above ,

2y ( 3x² + y²) -6y( x² – y²) = Ky²

6x²y +2y³ -6x²y +6y³ = Ky²

8y³ = Ky²

K = 8y

Q 14 – If a + b + c = 6 and ab + bc + ca = 11, find the value of a³ + b³ + c³ – 3abc.

Ans.

a³ + b³ + c³ – 3abc = (a + b + c) (a² + b² + c² – ab – bc – ca)

a³ + b³ + c³ – 3abc = (a+ b + c){(a² + b² + c²) – (ab + bc + ca)} …(i)

Clearly, we require the values of a + b+ c, a² + b² + c² and ab + bc + ca to obtain the value of a³ + b³ + c³ – 3abc.

We are given the values of a + b + c, ab + bc + ca. So, Let us first obtain the value of a² + b² + c².

We know that

(a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca

(a + b + c)² = (a² + b² + c²) + 2(ab + bc + ca)

6² = a² + b² + c² + 2 × 11 [putting the values of a + b + c and ab + bc + ca]

36 = a² + b² + c² + 22

a² + b² + c² = 36 – 22

a² + b² + c² = 14

Now, putting a + b + c = 6, ab + bc + ca = 1 and a² + b² + c² = 14 in (i), we get

a³ + b³ + c³ – 3abc = 6 × (14 – 11) = 6 × 3 = 18.

Q 15 – Evaluate the following by using identities: (1.5𝑥² – 0.3𝑦²) (1.5𝑥² + 0.3𝑦²)

Ans.

Take A = 1.5 x²

Take B = 0.3y²

& applying identity

(A + B) (A – B) = A² – B²

(A – B) × (A + B) = A² – B²

(1.5 x² – 0.3y²) (1.5x² + 0.3y²) = (1.5x²)² – (0.3y2)²= 2.25x⁴ – 0.09y⁴

Q 16 – Factorize: (𝑥²– 4𝑥)(𝑥²– 4𝑥 – 1) – 20

Ans.

Ans. We have,

(x²– 4x)(x² – 4x -1) – 20

= (x² – 4x)² – (x² – 4x) – 20

= y² – y – 20, where y = x² – 4x

= y² – 5y + 4y – 20

= (y² – 5y) + (4y – 20)

= y (y – 5) + 4(y – 5)

= (y – 5)(y + 4)

= (x² – 4x – 5) (x² – 4x + 4) [Replacing y by x² – 4x]

= (x² – 5x + x – 5) (x² – 2 × x × 2 + 2²)

= {x (x – 5) + (x – 5)} (x – 2)² = (x – 5) (x + 1) (x – 2)²

Back