Q 1 – The HCF of two numbers is 27 and their LCM is 162. If one of the numbers is 54, then the other number is
(a) 36
(b) 35
(c) 9
(d) 81
Q 2 – 225 can be expressed as
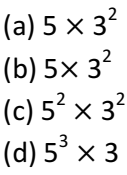

(a) an even number
(b) an odd number
(c) an odd prime number
(d) a prime number
Q 4. (n2 –1) is divisible by 8 if n is
(a) an integer
(b) a natural number
(c) an odd integer
(d) an even integer
Q 5 – Assertion: The HCF of two numbers is 5 and their product is 150, then their LCM is 30.
Reason : For any two positive integers a and b, HCF (a, b) + LCM (a, b) = a x b.
(a) Both assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and Reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
Q 6 – Find the HCF and LCM of 90 and 144 by the method of prime factorization.
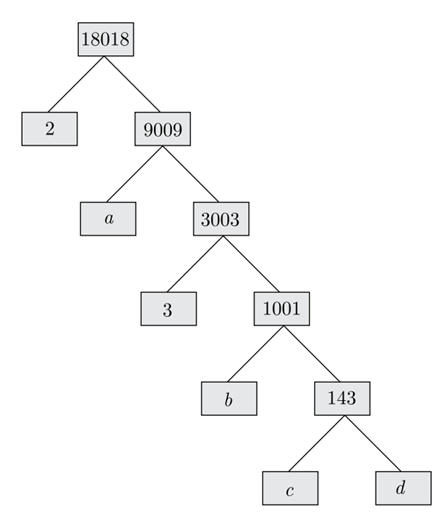
Q 7 – Find the missing numbers a, b, c and d in the given factor tree:
Q 8 – The length, breadth and height of a room are 8 m 50 cm, 6 m 25 cm and 4 m 75 cm respectively. Find the length of the longest rod that can measure the dimensions of the room exactly.
Q 9 – Show that 5 √6 is an irrational number.
Q 10 – An army contingent of 612 members is to march behind an army band of 48 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march?
Q 11 – Prove that 2 + 5 √3 is an irrational number, given that 3 is an irrational number.
Q 12 – Show that numbers 8n can never end with digit 0 of any natural number n.
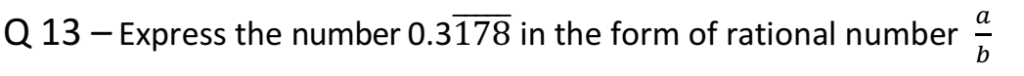
Q 14 – If p is prime number, then prove that √p is an irrational.
Q 15 – Prove that n 2– n is divisible by 2 for every positive integer n.