Triangles For Class 10 Maths Important Questions
Q 1 – In triangle PQR, if PQ = 6 cm, PR = 8 cm, QS = 3 cm, and PS is the bisector of angle QPR, what is the length of SR?
(A) 2
(B) 4
(C) 6
(D) 8
(B) 4
Q 2 – ABCD is a trapezium in which AB|| DC and P, Q are points on AD and BC respectively such that PQ || DC. If PD = 18 cm, BQ = 35 cm and QC = 15 cm, find AD.
(A) 55cm
(B) 57cm
(C) 60cm
(D) 62cm
(C) 60cm
Q 3 – Areas of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the larger triangle is 20 cm, then the length of the corresponding side of the smaller triangle is:
(A) 12cm
(B) 13cm
(C) 14cm
(D) 15cm
(A) 12cm
Q 4 – The areas of two similar triangles ABC and PQR are in the ratio 9:16. If BC = 4.5 cm, then the length of QR is
(A) 4 cm
(B) 4.5 cm
(C) 3 cm
(D) 6cm
(D) 6cm
Q 5 – The area of a right angled triangle is 40 sq cm and its perimeter is 40 cm. The length of its hypotenuse is
(A) 16 cm
(B) 18 cm
(C) 17 cm
(D) data insufficient
(B) 18 cm
Q 6 – Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
(A) 2:3
(B) 4:9
(C) 81:16
(D) 16 : 81
(D) 16 : 81
Q 7 – In the figure given below DE || BC. If AD = x, DB = x – 2, AE = x + 2 and EC = x – 1, the value of x is:
(A) 4
(B) 8
(C) 16
(D) 32
(A) 4
Q 8 – The length of altitude of an equilateral triangle of side 8cm is
(A) √3 cm
(B) 2√3 cm
(C) 3√3 cm
(D) 4√3cm
(D) 4√3cm
Q 9 – A 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then the distance by which the top of the ladder would slide upwards on the wall is:
(A) 2 m
(B) 1.2 m
(C) 0.8 m
(D) 0.5 m
(D) 4√3cm
Q 11 – The area of two similar triangle are respectively 25cm and 81 cm. Find the ratio of their corresponding sides.
Q 12 – IfΔABC is similar to ΔPQR such that AB = 1.4cm and PQ = 1.8cm. Find the ratio of ar (ΔABC) and ar (ΔPQR).
Q 13 – In the given figure, find MLN.
Q 14 – In the given figure, D and E are points on sides AC and AB of DABC such that B = ADE, show that DABC is similar to DADE.
. GIVEN:
∠B = ∠AED
In the following figure we have ∆ABC & ∆AED in which,
∠ABC = ∠AED (GIVEN)
∠BAC = ∠EAD (COMMON)
∆ABC ~ ∆AED
[ By AA criterion of Similarity ]
Hence, ∆ABC ~ ∆AED
Q 15 – In the given figure PQ is parallel to BC and CP is parallel to QR prove that AP2= AR x AB.
In figure PQ//BC AND CP//QR
THEN
first we have PQ//BC
>AP/AB=AQ/AC …. ..(1)( BY THELIS THEORY)
again
CP//QR
>AR/AP=AQ/AC……(2)
from (1) &(2)
>AP/AB=AR/AP
>AP^2=AR×AB
Q 16 – Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting AC in L and AD produced in E. Prove that EL = 2BL.
So, DE = BC (Corresponding parts of congruent triangles)
Also, AD = BC (Opposite sides of a parallelogram)
→ AE = AD + DE = 2BC
Now, ∠ 1 = ∠ 6 and ∠ 4 = ∠ 5
Q 17 – A 15 m high tower casts a shadow 24 m long at a certain time and at the same time , a telephone pole casts a shadow 16 m long. Find the height of the telephone pole.
From the question, it is given that,
Height of a tower PQ=15m
Its shadow QR=24 m
Let us assume the height of a telephone pole MN=x
Its shadow NO=16m
Given, at the same time,
△PQR∼△MNO
Therefore, PQ/MN=ON/RQ
15/x=24/16
By cross multiplication we get,
x=(15×16)/24
x=240/24
x=10
Therefore, height of pole =10m.
Q 18 – A and B are respectively the points on the sides PQ and PR of a ΔPQR such that PQ = 12.5 cm, PA = 5 cm, BR = 6 cm and PB = 4 cm. Is AB || QR ?
From the dimensions given in the question,
Consider the △PQR
So, PQ/PA=12.5/5
= 2.5/1
PR/PB=(PB+BR)/PB
=(4+6)/4
=10/4
=2.5
By comparing both the results,
2.5=2.5
Therefore, PQ/PA=PR/PB
So, AB is parallel to QR.
Q 19 – In ∆DEW, AB || EW. If AD = 4 cm, DE = 12 cm and DW = 24 cm, then find the value of DB.
Let BD = x cm,
Then, BW = (24−x) cm and AE = 12− 4 = 8cm
In ΔDEW, AB is parallel to EW
Q 20 – In a quadrilateral ABCD, B = 90 , AD2 = AB2 + BC2 + CD2, prove that ACD = 90
. As ∠ ABC =90∘
So applying Pythagoras theorem in △ABC
AB2 + BC2 = AC2 _____________(i)
Given AD2 = AB2 + BC2 + CD2 (2)
Substituting (1) in (2)
AD2 = AC2 + CD2
In △ACD , applying converse of Pythagoras theorem which states that if the square of the length of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle.
Q 21 – The areas of two similar triangles are 81 cm2 and 49 cm2 respectively. Find the ratio of their corresponding heights and ratio of their corresponding medians.
Given : Area of two similar triangles is 81cm² and 49cm² .
(i) Since, the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding altitudes.
ar(∆1)/ar(∆2) = (altitude 1/ altitude 2)²
81/49 = (altitude 1/ altitude 2)²
On taking square root on both sides,
√81/49 = √(altitude 1/ altitude 2)²
9/7 = altitude 1/ altitude 2
Altitude 1: altitude 2 = 9 : 7
Q 22 – Assertion: ABC and DEF are two similar triangles such that BC = 4 cm, EF = 5 cm and area of ABC = 64 cm2 then area of DEF = 100 cm2
Reason: The areas of two similar triangles are in the ratio of the squares of the corresponding altitudes.
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) If Assertion (A) is False but reason (R) is True.
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
Q 23 – In Figure, DE || BC . Find the length of side AD, given that AE = 1 8 . , cm BD = 7 2 . cm and CE = 5 4 . cm
Using basic proportionality theorem, we have
AD/BD =AE/CE
→ AD/7.2cm =1.8 cm/5.4cm
→ AD = 1.8 7.2/5.4 =2.4 cm
Thus, the length of the side AD is 2.4 cm.
Q 24 – In ABCD , |EB| , C find the value of x .
Q 25 – Fill in the Blanks:
- The perimeters of two similar triangles are 25 cm and 15 cm respectively. If one side of the first triangle is 9 cm, then the corresponding side of second triangle is ______.
- Two triangles are similar if their corresponding sides are _________.
- ABC is an equilateral triangle of side 2a, then length of one of its altitude is _______ .
- The corresponding sides of two similar triangles are in the ratio 3 : 4, then the ratio of the areas of triangles is _________ .
(a) 5.4 cm
(b) in proportion
(c) √3a
(d) 9:16.
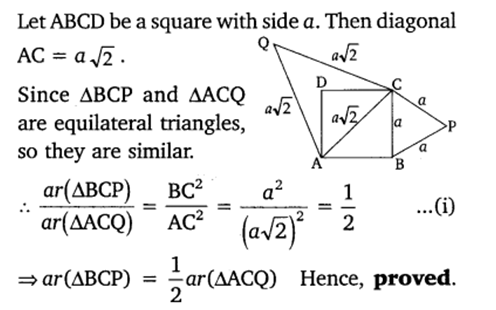
Q 26 – In the given figure, P and Q are points on the sides AB and AC respectively of a triangle ABC . PQ is parallel to BC and divides the triangle ABC into 2 parts, equal in area. What is the ratio of AP : AB ?
Q 27 – O is a point on side PQ of a APQR such that PO = QO = RO, then
(a) RS² = PR × QR
(b) PR² + QR² = PQ²
(c) QR² = QO² + RO²
(d) PO² + RO² = PR²
(b) PR² + QR² = PQ²
Q 28 – If ΔABC ~ ΔDEF and ΔABC is not similar to ΔDEF then which of the following is not true?
(a) BC.EF = AC.FD
(b) AB.ED = AC.DE
(c) BC.DE = AB.EE
(d) BC.DE = AB.FD
(c) BC.DE = AB.EE
Q 29 – In a rhombus if d1 = 16 cm, d2 = 12 cm, then the length of the side of the rhombus is
(a) 8 cm
(b) 9 cm
(c) 10 cm
(d) 12 cm
(c) 10 cm
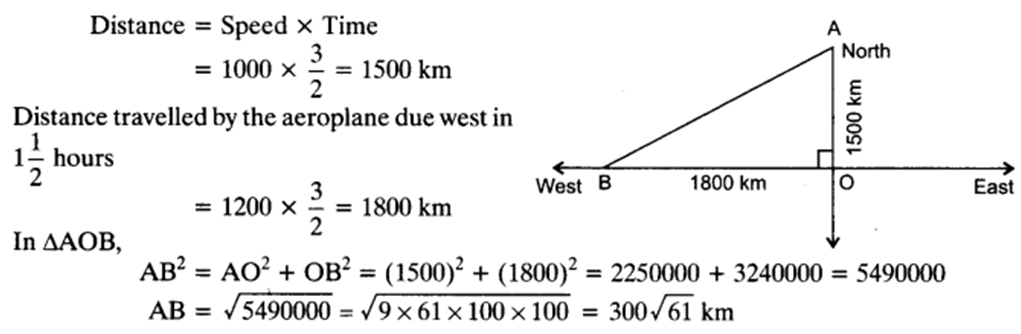
Q 30 – An aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after 1 hours?
Q 31 – Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
Q 32 – If the areas of two similar triangles are equal, prove that they are congruent.
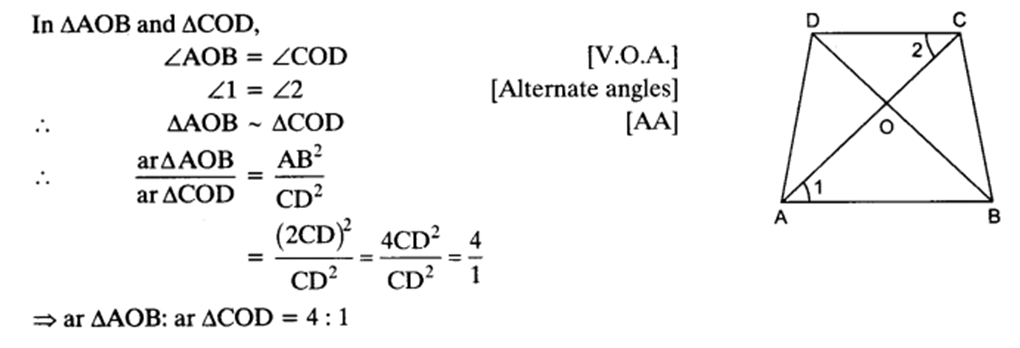
Q 33 – Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.
ABCD is a trapezium with AB II DC and AB = 2 CD
Q 34 – Let ∆ABC ~ ∆DEF and their areas be, respectively, 64 cm2 and 121 cm2. If EF = 15.4 cm, find BC.
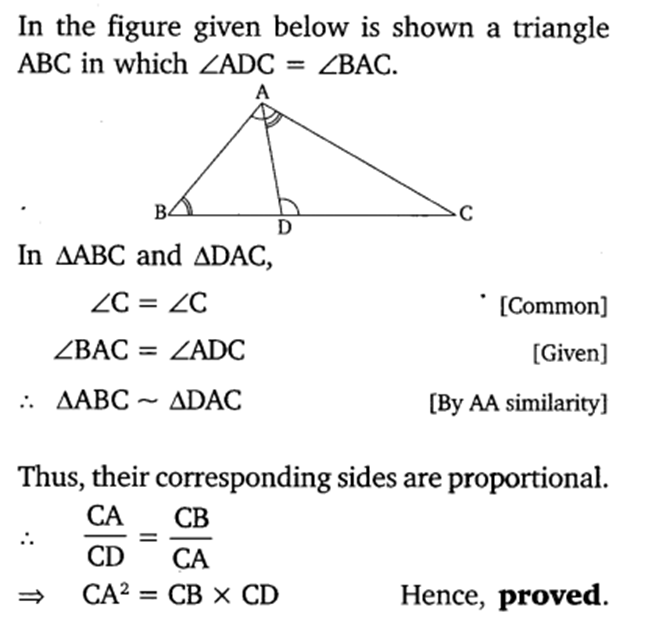
Q 35 – D is a point on the side BC of a triangle ABC, such that ∠ADC = ∠BAC. Show that CA² = CB.CD.